Sócrates [469 a.C. – 399 a.C.]
Sócrates (em grego: Σωκράτης, IPA: [sɔːkrátɛːs], transl. Sōkrátēs; Alópece, c. 469 a.C. – Atenas, 399 a.C.) foi um filósofo ateniense do período clássico da Grécia Antiga. Creditado como um dos fundadores da filosofia ocidental, é até hoje uma figura enigmática, conhecida principalmente através dos relatos em obras de escritores que viveram mais tarde, especialmente dois de seus alunos, Platão e Xenofonte, bem como pelas peças teatrais de seu contemporâneo Aristófanes. Muitos defendem que os diálogos de Platão seriam o relato mais abrangente de Sócrates a ter perdurado da Antiguidade aos dias de hoje.
Através de sua representação nos diálogos de seus estudantes, Sócrates tornou-se renomado por sua contribuição no campo da ética, e é este Sócrates platônico que legou seu nome a conceitos como a ironia socrática e o método socrático (elenchus). Este permanece até hoje a ser uma ferramenta comumente utilizada numa ampla gama de discussões, e consiste de um tipo peculiar de pedagogia no qual uma série de questões são feitas, não apenas para obter respostas específicas, mas para encorajar também uma compreensão clara e fundamental do assunto sendo discutido. Foi o Sócrates de Platão que fez contribuições importantes e duradouras aos campos da epistemologia e da lógica, e a influência de suas ideias e de seu método continuam a ser importantes alicerces para boa parte dos filósofos ocidentais que se seguiram a ele.
Nas palavras do filósofo britânico Martin Cohen, Platão, o idealista, oferece “um ídolo, a figura de um mestre, para a filosofia. Um santo, um profeta do ‘Deus-Sol’, um professor condenado por seus ensinamentos como herege”.
Sua Vida
Nascido nas planícies do monte Licabeto, próximo a Atenas, Sócrates vinha de família humilde. Era filho de Sofronisco – motivo pelo qual ele era chamado em sua juventude de Sokrates ios Sōfronískos (Sócrates, o filho de Sofronisco) -, um escultor, especialista em entalhar colunas nos templos, e Fainarete, uma parteira (ambos eram parentes de Aristides, o Justo).
Durante sua infância, ajudou seu pai no ofício de escultor. Porém, muitas vezes, seus amigos zombavam da sua incapacidade de trabalhar o mármore. Mesmo quando aparecia uma oportunidade de ajudar o seu pai, sempre acabava atrapalhando. Seu destino foi apontado, pelo próprio Oráculo de Delfos, como o de ser um grande educador, mas foi somente por influência da sua mãe que ele pôde descobrir sua verdadeira vocação.
Sócrates foi casado com Xântipe, que era bem mais jovem que ele, e teve com ela um filho, Lamprocles. Porém, segundo Aristóteles e seu discípulo Aristóxenes, Sócrates teria tido outra esposa, Mirto, com quem teve os filhos Sofronisco e Menexêno. Segundo relato posterior de Diógenes Laércio, ela teria sido a segunda esposa e era filha de Aristides, o Justo. Sátiro e Jerônimo de Rodes, também citados por Diógenes Laércio, dizem que, pela falta de homens em Atenas, era permitido a um ateniense casado ter filhos com outra mulher, e que Sócrates teria tido Xântipe e Mirto ao mesmo tempo. Armand D’Angour argumenta que Mirto fora na verdade a primeira esposa de Sócrates, conforme evidenciado pela sua omissão nos relatos de Xenofonte e Platão, que eram jovens quando encontraram com um Sócrates em idade adulta avançada e nem a teriam conhecido.
Seu amigo Críton criticou-o por ter abandonado seus filhos quando se recusou a tentar fugir para evitar sua execução. Este fato mostra que ele (assim como outros discípulos) não teria entendido a mensagem que Sócrates passa sobre a morte (diálogo Fédon).
Sócrates costumava caminhar descalço, não tinha o hábito de tomar banho e amava livros sobre sexologia. Em certas ocasiões, parava o que quer que estivesse fazendo, ficava imóvel por horas, meditando sobre algum problema. Certa vez o fez descalço sobre a neve, segundo os escritos de Platão, o que demonstra seu caráter lendário.
Cláudio Eliano lista Sócrates como um dos grandes homens que gostavam de brincar com crianças: uma vez, Alcibíades surpreendeu Sócrates brincando com seu filho Lamprocles.
Biografia
Detalhes sobre a vida de Sócrates derivam de três fontes contemporâneas: os diálogos de Platão, as peças de Aristófanes e os diálogos de Xenofonte. Não há evidência de que Sócrates tenha ele mesmo publicado alguma obra. Alguns autores defendem que ele não deixou nada escrito pois, além de na sua época a transmissão do saber ser feita, essencialmente, pela via oral, Sócrates assumia-se como alguém que sabe que nada sabe. Assim, para ele, a escrita fecharia o conhecimento, deixando-o de forma acabada, amarrando o seu autor ao estrito contexto de afirmações inamovíveis: se essas afirmações contemplam o erro, a escrita não só o perpetua como garante a sua transmissão.
As obras de Aristófanes retratam Sócrates como um personagem cômico e sua representação não deve ser levada ao pé da letra.
Vocação
Conta-se que, um dia, Sócrates foi levado junto à sua mãe para ajudar em um parto complicado. Vendo sua mãe realizar o trabalho, Sócrates logo filosofou: Minha mãe não irá criar o bebê, apenas ajudá-lo-á a nascer e tentará diminuir a dor do parto. Ao mesmo tempo, se ela não tirar o bebê, logo ele irá morrer, e igualmente a mãe morrerá!
Sócrates concluiu, então, que, de certa forma, ele também era um parteiro. O conhecimento está dentro das pessoas (que são capazes de aprender por si mesmas). Porém, eu posso ajudar no nascimento deste conhecimento. Concluiu ele. Por isso, até hoje os ensinamentos de Sócrates são conhecidos por maiêutica (que significa parteira em grego).
Assim, logo sua vocação falou mais alto e ele partiu para aprender filosofia, vindo a ser discípulo dos filósofos Anaxágoras e Arquelau. Seu talento logo chamou a atenção. Tanto que foi chamado pela Pítia (sacerdotisa do templo de Apolo, em Delfos, na Antiga Grécia) de o mais sábio de todos os homens!
Trabalho
Não se sabe ao certo qual o trabalho de Sócrates, se é que ele teve outro além da filosofia. De acordo com algumas fontes, Sócrates aprendeu a profissão de oleiro com seu pai. Na obra de Xenofonte, Sócrates aparece declarando que se dedicava àquilo que ele considerava a arte ou ocupação mais importante: maiêutica, o parto das ideias. A maiêutica socrática funcionava a partir de dois momentos essenciais: um primeiro em que Sócrates levava os seus interlocutores a pôr em causa as suas próprias concepções e teorias acerca de algum assunto; e um segundo momento em que conduzia os interlocutores a uma nova perspectiva acerca do tema em abordagem. Daí que a maiêutica consistisse num autêntico parto de ideias, pois, mediante o questionamento dos seus interlocutores, Sócrates levava-os a colocar em causa os seus preconceitos acerca de determinado assunto, conduzindo-os a novas ideias acerca do tema em discussão, reconhecendo, assim, a sua ignorância e gerando novas ideias, mais próximas da verdade.
Sócrates defendia que deve-se sempre dar mais ênfase à procura do que não se sabe, do que transmitir o que se julga saber, privilegiando a investigação permanente.
Sócrates tinha o hábito de debater e dialogar com as pessoas de sua cidade. Ao contrário de seus predecessores, ele não fundou uma escola, preferindo também realizar seu trabalho em locais públicos (principalmente nas praças públicas e ginásios), agindo de forma descontraída e descompromissada, dialogando com todas as pessoas, o que fascinava jovens, mulheres e políticos de sua época.
Platão afirma que Sócrates não recebia pagamento por suas aulas. Sua pobreza era prova de que não era um sofista.
Várias fontes, inclusive os Diálogos de Platão, mencionam que Sócrates tinha servido ao exército em várias batalhas. Na Apologia de Sócrates, Sócrates compara seu período no serviço militar a seus problemas no tribunal, e diz que qualquer pessoa no júri que imagine que ele deveria se retirar da filosofia deveria também imaginar que os soldados devessem bater em retirada quando era provável que pudessem morrer em uma batalha. Estrabão conta que, após uma derrota ateniense em que Sócrates e Xenofonte haviam perdido seus cavalos, Sócrates encontrou Xenofonte caído no chão, e carregou-o por vários estádios, até que a batalha terminou.
Do Julgamento à Morte
“Eu predigo-vos portanto, a vós juízes, que me fazeis morrer, que tereis de sofrer, logo após a minha morte, um castigo muito mais penoso, por Zeus, que aquele que me infligis matando-me. Acabais de condenar-me na esperança de ficardes livres de dar contas de vossas vidas; ora é exatamente o contrário que vos acontecerá, asseguro-vos (…) Pois se vós pensardes que matando as pessoas, impedireis que vos reprovem por viverem mal, estais em erro. Esta forma de se desembaraçarem daqueles que criticam não é nem muito eficaz nem muito honrosa.” Sócrates
O julgamento e a execução de Sócrates são eventos centrais da obra de Platão (Apologia e Críton). Sócrates admitiu que poderia ter evitado sua condenação a morte, bebendo antes o veneno chamado cicuta, se tivesse desistido da vida justa. Mesmo depois de sua condenação, ele poderia ter evitado sua morte se tivesse escapado com a ajuda de amigos.
Platão considerou que Sócrates foi condenado por questões evidentemente políticas. Por seu lado, Xenofonte atribuiu a acusação a Sócrates a um fato de ordem pessoal, pelo desejo de vingança. O propósito não era a morte de Sócrates mas sim afastá-lo de Atenas e se isso não ocorreu deveu-se à teimosia de Sócrates.
Julgamento
Tão logo as ideias de Sócrates foram se espalhando pela cidade, ele ganhava mais e mais discípulos.
Assim, pensavam eles: Como um homem poderia ensinar de graça e pregar que não se precisavam de professores como eles?. E mais: Eles não concordavam com os pensamentos de Sócrates, que dizia que para se acreditar em algo, era preciso verificar se aquilo realmente era verdade.
Logo, Sócrates começou a fazer vários inimigos, assim causando uma grande intriga. Mas eis que a guerra do Peloponeso estourou, todos os homens entre 15 e 45 anos de idade foram enviados para lutar. Sócrates, pela sua habilidade de fazer as pessoas o seguirem, foi escolhido então como um dos generais.
Ao final da guerra, com a intenção de salvar os poucos soldados que estavam vivos, Sócrates ordena que todos voltem rapidamente para Atenas, mas deixassem os mortos no campo de batalha – contrariando uma lei que obrigava o general a enterrar todos os seus soldados mortos, ou morrer tentando. Assim, ao chegar, ele é preso.
Usando toda a sua capacidade de persuasão, Sócrates consegue convencer a todos de que era melhor deixar alguns mortos do que morrerem todos, uma vez que se todos morressem, ninguém poderia enterrá-los. Desta forma, ele consegue a liberdade.
Ficou livre por mais 30 anos, quando foi preso novamente, acusado de 3 crimes:
1- Não acreditar nos costumes e nos deuses gregos;
2- Unir-se a deuses malignos que gostam de destruir as cidades;
3- Corromper jovens com suas ideias.
Os acusadores foram: Ânito, Meleto e Lícon.
Ânito – era um líder democrático. Tinha um filho discípulo de Sócrates que ria dos deuses do pai e voltava-se contra eles. Representava a classe dos políticos. Era um rico tanoeiro que representava os interesses dos comerciantes e industriais, era poderoso e influente.
Meleto – era um poeta trágico novo e desconhecido. Foi o acusador oficial, porém nada exigia que ele como acusador oficial fosse o mais respeitável, hábil ou temível, mas somente aquele que assinava a acusação. Representava a classe dos poetas e adivinhos.
Lícon – Pouco se sabe de Lícon. Era um retórico obscuro e o seu nome teve pouca importância e autoridade no decorrer da condenação de Sócrates. Representava a classe dos oradores e professores de retórica. Talvez Lícon pretendesse a condenação de Sócrates, devido ao seu filho ter-se deixado corromper moralmente, filosoficamente e sexualmente por Callias, e Callias era um associado de Sócrates.
Estas 3 acusações foram assim proferidas por Meleto:
“…Sócrates é culpado do crime de não reconhecer os deuses reconhecidos pelo Estado e de introduzir divindades novas; ele é ainda culpado de corromper a juventude. Castigo pedido: a morte”
Condenação
“O processo e a condenação de Sócrates testemunham o perigo que a ignorância faz correr ao saber, que o mal faz correr à virtude. Mas este perigo não é senão aparente, pois, na realidade, é o justo que triunfa dos seus carrascos. Se bem que seja vítima deles, o triunfo de Sócrates sobre os seus juízes data do dia da sua execução.” (Jean Brun)
Dada, a ele, a chance de se defender destas acusações, Sócrates mostra toda a sua capacidade de pensamento.
Em sua defesa, ele mostra que as acusações eram contraditórias, questionando: Como posso não acreditar nos deuses e ao mesmo tempo me unir a eles?.
Mesmo assim, o tribunal, constituído por 501 cidadãos, o condenou. Mas não à morte, pois sabiam que se o condenassem à morte, milhares de jovens iriam se revoltar. Condenaram-no a se exilar para sempre, ou a lhe ser cortada a língua, impossibilitando-o assim de ensinar aos demais. Caso se negasse, ele seria morto.
Após receber sua sentença, Sócrates proferiu: – Vocês me deixam a escolha entre duas coisas: uma que eu sei ser horrível, que é viver sem poder passar meus conhecimentos adiante. A outra, que eu não conheço, que é a morte … escolho pois o desconhecido!
Morte
“Mas eis a hora de partir: eu para a morte, vós para a vida. Quem de nós segue o melhor rumo, ninguém o sabe, exceto os deuses.”
Ao se dirigir aos atenienses que o julgaram, Sócrates disse que lhes era grato e que os amava, mas que obedeceria antes aos deuses do que a eles, pois, enquanto tivesse um sopro de vida, poderiam estar seguros de que não deixaria de filosofar, tendo, como sua única preocupação, andar pelas ruas a fim de persuadir seus concidadãos, moços e velhos, a não se preocupar nem com o corpo nem com a fortuna tão apaixonadamente quanto com a alma, a fim de torná-la tão boa quanto possível.
Sócrates, então, deixou o tribunal e foi para a prisão. Como existia uma lei que exigia que nenhuma execução acontecesse durante a viagem votiva de um navio sagrado a Delos, Sócrates ficou a ferros por 30 dias, sob custódia de onze magistrados encarregados em Atenas da polícia e da administração penitenciária.
Durante estes 30 dias, ele recebeu os seus amigos e conversou com eles. Declarando não querer absolutamente desobedecer às leis da pátria, Sócrates recusava a ajuda dos amigos para fugir. E passou o tempo preparando-se para o passo extremo em palestras espirituais com os amigos.
Chegado o momento da execução, pouco antes de beber o veneno, Sócrates, de forma irônica e sarcástica (como de costume), proferiu suas últimas palavras:
“Críton, somos devedores de um galo a Asclépio; pois bem, pagai a minha dívida. Pensai nisso!”
Após essas palavras, Sócrates bebeu a cicuta (Conium maculatum) e, diante dos amigos, aos 70 anos, morreu por envenenamento.
Platão, no seu livro Fédon, assim narrou a morte de seu mestre:
Depois de assim falar, levou a taça aos lábios e, com toda a naturalidade, sem vacilar um nada, bebeu até à última gota.
Até esse momento, quase todos tínhamos conseguido reter as lágrimas; porém quando o vimos beber, e que havia bebido tudo, ninguém mais aguentou. Eu também não me contive: chorei à lágrima viva. Cobrindo a cabeça, lastimei o meu infortúnio; sim, não era por desgraça que eu chorava, mas a minha própria sorte, por ver de que espécie de amigo me veria privado. Critão levantou-se antes de mim, por não poder reter as lágrimas. Apolodoro, que, desde o começo, não havia parado de chorar, pôs-se a urrar, comovendo, seu pranto e lamentações, até o íntimo de todos os presentes, com exceção do próprio Sócrates.– Que é isso, gente incompreensível? Perguntou. Mandei sair as mulheres, para evitar esses exageros. Sempre soube que só se deve morrer com palavras de bom agouro. Acalmai-vos! Sede homens!
Ouvindo-o falar dessa maneira, sentimo-nos envergonhados e paramos de chorar. E ele, sem deixar de andar, ao sentir as pernas pesadas, deitou-se de costas, como recomendara o homem do veneno. Este, a intervalos, apalpava-lhe os pés e as pernas. Depois, apertando com mais força os pés, perguntou se sentia alguma coisa. Respondeu que não. De seguida, sem deixar de comprimir-lhe a perna, do artelho para cima, mostrou-nos que começava a ficar frio e a enrijecer. Apalpando-o mais uma vez, declarou-nos que no momento em que aquilo chegasse ao coração, ele partiria. Já se lhe tinha esfriado quase todo o baixo-ventre, quando, descobrindo o rosto – pois o havia tapado antes – disse, e foram suas últimas palavras:
– Critão (exclamou ele), devemos um galo a Asclépio. Não te esqueças de saldar essa dívida!
“Assim farei!”, respondeu Critão. Vê se queres dizer mais alguma coisa. A essa pergunta, já não respondeu. Decorrido mais algum tempo, deu um estremeção. O homem o descobriu; tinha o olhar parado. Percebendo isso, Critão fechou-lhe os olhos e a boca.
Tal foi o fim do nosso amigo, Equécrates, do homem, podemos afirmá-lo, que entre todos os que nos foi dado conhecer, era o melhor e também o mais sábio e mais justo.
No Fédon, Sócrates dá razões para crer na imortalidade. Quando Sócrates foi condenado à morte, comentou, alegremente, que, no outro mundo, poderia fazer perguntas eternamente sem ser condenado a morrer, porque era imortal.
Ruptura e legado
Sócrates provocou uma ruptura sem precedentes na história da Filosofia grega, por isso ela passou a considerar os filósofos entre pré-socráticos e pós-socráticos. Enquanto os filósofos pré-Socráticos, chamados de naturalistas, procuravam responder a questões do tipo: “O que é a natureza ou o fundamento último das coisas?” Sócrates, por sua vez, procurava responder à questão: “O que é a natureza ou a realidade última do homem?”.
Os sofistas, grupo de filósofos (título negado por Platão) originários de várias cidades, viajavam pelas pólis, onde discursavam em público e ensinavam suas artes, como a retórica, em troca de pagamento. Sócrates se assemelhava exteriormente a eles, exceto no pensamento. Platão afirma que Sócrates não recebia pagamento por suas aulas. Sua pobreza era prova de que não era um sofista. Para os sofistas, tudo deveria ser avaliado segundo os interesses do homem e da forma como este vê a realidade social (subjetividade), segundo a máxima de Protágoras :“O homem é a medida de todas as coisas, das coisas que são, enquanto são, das coisas que não são, enquanto não são”. Isso significa que, segundo essa corrente de pensamento, as regras morais, as posições políticas e os relacionamentos sociais deveriam ser guiados conforme a conveniência individual. Para este fim, qualquer pessoa poderia se valer de um discurso convincente, mesmo que falso ou sem conteúdo. Os sofistas usavam, de fato, complicados jogos de palavras, no discurso para demonstrar a verdade daquilo que se pretendia alcançar. Este tipo de argumento ganhou o nome de sofisma.
Em resumo, a sofística destruía os fundamentos de todo conhecimento, já que tudo seria relativo (relativismo) e os valores seriam subjetivos, assim como impedia o estabelecimento de um conjunto de normas de comportamento que garantissem os mesmos direitos para todos os cidadãos da pólis. Tanto quanto os sofistas, Sócrates abandonou a preocupação em explicar e se concentrou no problema do homem. No entanto, contrariamente aos sofistas, Sócrates travou uma polêmica profunda com estes, pois procurava um fundamento último para as interrogações humanas (“O que é o bem?” “O que é a virtude?” “O que é a justiça?”); enquanto os sofistas situavam as suas reflexões a partir dos dados empíricos, o sensório imediato, sem se preocupar com a investigação de uma essência da virtude, da justiça do bem etc., a partir da qual a própria realidade empírica pudesse ser avaliada.
Sócrates contribuiu para que as pessoas se apercebessem da descoberta da evidência que é a manifestação do mestre interior à alma. Conhecer-se a si mesmo seria conhecer Deus em si.
Aquilo que colocou Sócrates em destaque foi o seu método, e não tanto as suas doutrinas. Sócrates baseava-se na argumentação, insistindo que só se descobre a verdade pelo uso da razão. O seu legado reside sobretudo na sua convicção inabalável de que mesmo as questões mais abstratas admitem uma análise racional.
Filosofia
O seu pensamento desenvolveu-se de 3 grandes ideias:
a) a crítica aos sofistas;
b) a arte de perguntar;
c) a consciência do Homem.
Método Socrático
O método socrático consiste em uma técnica de investigação filosófica, que faz uso de perguntas simples e quase ingênuas que têm, por objetivo, em primeiro lugar, revelar as contradições presentes na atual forma de pensar do aluno, normalmente baseadas em valores e preconceitos da sociedade, e auxiliá-lo assim a redefinir tais valores, aprendendo a pensar por si mesmo.
Ideias Filosóficas
As crenças de Sócrates, em comparação às de Platão, são difíceis de discernir. Há poucas diferenças entre as duas ideias filosóficas. Consequentemente, diferenciar as crenças filosóficas de Sócrates, Platão e Xenofonte é uma tarefa difícil e deve-se sempre lembrar que o que é atribuído a Sócrates pode refletir o pensamento dos outros autores.
Se algo pode ser dito sobre as ideias de Sócrates, é que ele foi moralmente, intelectualmente e filosoficamente diferente de seus contemporâneos atenienses. Quando estava sendo julgado por heresia e por corromper a juventude, usou seu método de elenchos para demonstrar as crenças errôneas de seus julgadores. Sócrates acreditava na imortalidade da alma e que teria recebido, em um certo momento de sua vida, uma missão especial do deus Apolo Apologia, a defesa do logos apolíneo “conhece-te a ti mesmo”.
Sócrates também duvidava da ideia sofista de que a arete (virtude) podia ser ensinada para as pessoas. Acreditava que a excelência moral é uma questão de inspiração e não de parentesco, pois pais moralmente perfeitos não tinham filhos semelhantes a eles. Isso talvez tenha sido a causa de não ter se importado muito com o futuro de seus próprios filhos. Sócrates frequentemente dizia que suas ideias não eram próprias, mas de seus mestres, entre eles Pródico e Anaxágoras de Clazômenas.
Amor
Em O Banquete, de Platão, Sócrates revela que foi a sacerdotisa Diotima de Mantinea que o iniciou nos conhecimentos e na genealogia do amor. As ideias de Diotima estão na origem do conceito socrático-platônico do amor. Também em O Banquete, no discurso de Alcibíades se descreve o amor entre Sócrates e Alcibíades.
Conhecimento
Sócrates dizia que sua sabedoria era limitada à sua própria ignorância. Segundo ele, a verdade, escondida em cada um de nós, só é visível aos olhos da razão (daí a célebre frase “Só sei que nada sei!”). Ele acreditava que os erros são consequência da ignorância humana. Nunca proclamou ser sábio. A intenção de Sócrates era levar as pessoas a conhecerem seus desconhecimentos (“Conhece-te a ti mesmo”). Através da problematização de conceitos conhecidos, daquilo que se conhece, percebem-se os dogmas e preconceitos existentes.
Virtude
O estudo da virtude se inicia na chamada ética das virtudes com Sócrates, para quem a virtude é o fim da atividade humana e se identifica com o bem que convém à natureza humana.
Sócrates acreditava que o melhor modo para as pessoas viverem era se concentrando no próprio desenvolvimento ao invés de buscar a riqueza material. Convidava outros a se concentrarem na amizade e em um sentido de comunidade, pois acreditava que esse era o melhor modo de se crescer como uma população. Suas ações são provas disso: ao fim de sua vida, aceitou a sentença de morte quando todos acreditavam que fugiria de Atenas, pois acreditava que não podia fugir de sua comunidade. Acreditava que os seres humanos possuíam certas virtudes, tanto filosóficas quanto intelectuais. Dizia que a virtude era a mais importante de todas as coisas.
Política
Diz-se que Sócrates acreditava que as ideias pertenciam a um mundo que somente os sábios conseguiam entender, fazendo com que o filósofo se tornasse o perfeito governante para um Estado. Opunha-se à democracia aristocrática que era praticada em Atenas durante sua época; essa mesma ideia surge nas Leis de Platão, seu discípulo. Sócrates acreditava que, ao se relacionar com os membros de um parlamento, a própria pessoa estaria fazendo-se hipócrita.
O Sócrates também foi a favor de uma burocracia eleita, em detrimento de uma burocracia por sorteio:
[Foi] considerado que esta forma de nomeação de magistrados (isto é, as eleições) também foi mais democrático do que o vazamento de lotes, uma vez que, no âmbito do plano de eleição por sorteio, oportunidade decidiria a questão e os partidários da oligarquia, muitas vezes, obtêm os escritórios; Considerando que, no âmbito do plano de selecionar os homens dignos, as pessoas têm, em suas mãos, o poder de escolher aqueles que estavam mais ligados à constituição existente.
[Sócrates] ensinou aos seus companheiros a desprezar as leis estabelecidas insistindo na loucura de nomeação de funcionários públicos por sorteio, quando nenhum iria escolher um piloto ou construtor ou flautista por sorteio, nem qualquer outro artesão de trabalho em que os erros são muito menos desastrosos do que erros na arte de governar.
41 Frases de Sócrates – Filósofo e Pensador
Tudo o que sei, é que nada sei!
O verdadeiro conhecimento vem de dentro.
Para conseguir a amizade de uma pessoa digna é preciso desenvolvermos em nós mesmos as qualidades que naquela admiramos.
Deve-se temer mais o amor de uma mulher do que o ódio de um homem.
Sábio é aquele que conhece os limites da própria ignorância.
Uma vida sem desafios não vale a pena ser vivida.
O amigo deve ser como o dinheiro, cujo valor já conhecemos antes de termos necessidade dele.
Conhece-te a ti mesmo e conhecerás o universo e os deuses.
Meu conselho é que se case. Se você arrumar uma boa esposa, será feliz; se arrumar uma esposa ruim, se tornará um filósofo.
Existe apenas um bem, o saber, e apenas um mal, a ignorância.
Sob a direção de um forte general, não haverá jamais soldados fracos.
Aquilo que não puderes controlar, não ordenes.
Não penses mal dos que procedem mal; pensa somente que estão equivocados.
A sabedoria começa na reflexão.
Três coisas devem ser feitas por um juiz: ouvir atentamente, considerar sobriamente e decidir imparcialmente.
Não vivemos para comer, mas comemos para viver.
Creio que tenho prova suficiente de que falo a verdade: a pobreza.
Mas eis a hora de partir: eu para morte, vós para a vida. Quem de nós segue o melhor rumo ninguém o sabe, exceto os deuses.
A vida sem ciência é uma espécie de morte.
O homem faz o mal, porque não sabe o que é o bem.
A maneira de se conseguir boa reputação reside no esforço em se ser aquilo que se deseja parecer.
Se alguém procura a saúde, pergunta-lhe primeiro se está disposto a evitar no futuro as causas da doença; em caso contrário, abstém-te de o ajudar.
A um homem bom não é possível que ocorra nenhum mal, nem em vida nem em morte.
Quanto mais sei que sei, menos sei que sei.
Conhece-te a ti mesmo, torna-te consciente de tua ignorância e serás sábio.
Aquele a quem a palavra não educar, também o pau não educará.
O próprio sábio cora das suas palavras, quando elas surpreendem as suas ações.
Se alguém mente sobre você, faça o contrário para que ele se passe por mentiroso.
Transforme as pedras que você tropeça nas pedras de sua escada.
Se o desonesto soubesse a vantagem de ser honesto, ele seria honesto ao menos por desonestidade.
Só quem entende a beleza do perdão pode julgar seus semelhantes.
A palavra é o fio de ouro do pensamento.
Seja um homem sério, brinque.
A mentira nunca vive o suficiente para envelhecer.
Melhor sofrer uma injustiça do que cometê-la.
Quem melhor conhece a verdade é mais capaz de mentir.
Só é útil o conhecimento que nos torna melhores.
Todo o meu saber consiste em saber que nada sei.
O amor não é um deus, nem um mortal, e sim um grande demônio.
Inteligente é aquele que sabe que não sabe nada.
O homem para ser completo tem que estudar, trabalhar e lutar.
Frases de Pensadores da História

“Nosso caráter é resultado de nossa conduta”. Aristóteles
“é lícito afirmar que são prósperos os povos cuja legislação se deve aos filósofos”. Aristóteles
“Nunca vista suas melhores calças quando sair para lutar pela liberdade e pela verdade”. Henrik Ibsen – dramaturgo norueguês 1828-1906
“Quanto menos inteligente um homem é, menos misteriosa lhe parece a existência”. Arthur Schopenhauer – filósofo alemão 1788-1860
“Há, verdadeiramente, duas coisas diferentes: saber e crer que se sabe. A ciência consiste em saber; em crer que se sabe está a ignorância”. Hipócrates – médico grego 460-377 a.C.
“A ignorância afirma ou nega veementemente; a ciência duvida”. Voltaire – filósofo francês 1694-1778
“Imagination is more important than knowledge”. “A Imaginação é mais importante que o conhecimento” Albert Einstein
“O Socialismo não produziu socialistas”. José Saramago
“é preciso viver, não apenas existir”. Plutarco
“A grande revolução da engenharia genética é que o homem não é só dono da natureza, mas também pode criar um ser vivo. Ele passou a ser proprietário dos mecanismos íntimos da criação”. Daniel Borrillo – Advogado italiano
“Nossa existência não é mais que um curto-circuito de luz entre duas eternidades de escuridão”. Vladimir Nabokov
“As idéias religiosas surgiram da mesma necessidade de que se originaram todas as outras realizações da civilização, ou seja, da necessidade de defesa contra a força esmagadoramente superior da natureza”. Freud
“Nunca ande pelo caminho traçado, pois ele conduz somente até onde os outros foram”. Alexandre Graham Bell
“Se a História fosse vista como um repositório para algo mais do que anedotas ou cronologias, poderia produzir uma transformação decisiva na imagem de ciência que atualmente nos domina”. Thomas S. Kuhn
“Os homens devem ter corrompido um pouco a natureza, pois não nasceram lobos e acabaram se tornando lobos”. Voltaire
“O que você tem capacidade de fazer, tem capacidade também de não fazer”. Aristóteles
“Em tudo o que fazemos, temos em vista alguma outra coisa”. Aristóteles
“A perfeição é feita de pequenos detalhes – não é apenas um detalhe”. Michelangelo
“Os ideais que iluminaram meu caminho e sempre me deram coragem para enfrentar a vida com alegria foram a Verdade, a Bondade e a Beleza”. Albert Einstein
“Deixe que cada um exercite a arte que conhece”. Aristóteles
“Estou convencido de que o mundo não é um mero pântano onde homens e mulheres se jogam… e morrem. Algo magnificente está ocorrendo aqui em meio ás crueldades e tragédias e o desafio supremo á inteligência é fazer prevalecer o que há de mais nobre e melhor em nossa curiosa herança”. Charles Austin Beard
“E os que foram maltratados e acreditam que foram maltratados são terríveis, pois estão sempre em busca de sua oportunidade”. Aristóteles
“O pensamento é a grandeza do homem”. (Pascal).
“Toda nossa ciência comparada a nossa realidade é primitiva e infantil, e no entanto, é a coisa mais preciosa que temos”. Albert Einstein
“Conservar algo que possa recordar-te seria admitir que eu pudesse esquecer-te”. Shakespeare
“Onde há muito sentimento, há muita dor”. Leonardo da Vinci
“Por mais longe que vá o espírito, nunca irá tão longe quanto o coração”. Sócrates
“Só existem dois dias no ano que nada pode ser feito. Um se chama ontem e o outro se chama amanhã, portanto, hoje é o dia certo para amar, acreditar, fazer e principalmente viver”. (Tenzin Gyatso, 14º Dalai Lama).
Frases de Pensadores Contemporâneos

“Cada momento da nossa vida é um ensaio para o que vem a seguir”. Marcio Giulierme
“Se a vida fosse um caminhão … você deixaria ela te atropelar ou ficaria vendo ela passar?”. Rocker
“O nosso destino é sempre tentar mudar o nosso próprio destino”. Rocker
“Se amar é viver, viva intensamente pra não se arrepender de não ter amado”. Danny
“Onde quer que você esteja você sempre estará lá”. Silvia C. S. Machado
“Depois de a última árvore sem frutos, o último rio envenenado, o homem perceberá que dinheiro não se come”. Gustavo de Assis
“Sonho que se sonha só, é só um sonho que se sonha só, mas sonho que se sonha junto é realidade”. Raul Seixas
“O “mundo”; anda pelo caminho procurando por Deus, mas o cristão anda com Deus pelo caminho”. Danny
“O dinheiro é o que tapa o buraco na alma de quem não tem nada a dizer”. Juan de Lucas
“Não importa a cor do sabão, a espuma sempre será branca”. Neyro R. Junior
“Se tens a Cristo, sorria na juventude…. na velhice… e eternamente”. Danny
“Nunca é impossível ajudar alguém que se encontra numa situação pior que você…”. Luiz Balbino
“O álcool é o maior inimigo do homem… e o homem que foge de seus inimigos é um covarde mas, melhor um covarde vivo, que um herói morto!”. Danny
“A vida é uma sucessão de sucessivos que sucedem sucessivamente sem cessar”. Autor desconhecido
Ou a Biblia afasta você do mundo ou o mundo afasta você da Bíblia… Danny
“Confie em Deus, mas tranque seu carro”. Dalai Lama
“é melhor viver dez anos de uma vida efervescente do que morrer aos setenta e ter passado a vida assistindo TV”. Janis Joplin
“A vida é bela, a gente é que acaba com ela!”. Thiago Parolin
“Os ignorantes, que acham que sabem tudo, privam-se de um dos maiores prazeres da vida: APRENDER”. Gustavo de Assis
“Viva intensamente cada segundo, pois se você parar para pensar, o amanhã não existirá, ele pertence a Deus”. Danny
“Há muitas coisas mais importantes que o dinheiro… mas elas custam caro!”. Gustavo Pasqual
“Poder não é mostrar o que você tem mas, ser capaz de mostrar que pode!”. Danny
“A estratégia é a ciência do emprego do tempo e do espaço. Sou menos avaro com o espaço do que com o tempo. O espaço, podemos reganhá-lo. O tempo perdido, jamais”. Bernardo Ortega
“Or the Bible moves you away of the world or the world moves you away of the Bible”. Danny
“Aprendemos com os anos muita coisa que os dias desconhecem”. Danny
“A vida é uma vai-e-vem que vai e não tem volta”. Eduardo Stulzer de Almeida
“The “world”; walks for the road seeking for God, but the christian walks with God for the road”. Danny
“A vida é como uma rodoviária… as pessoas vêm e vão a todo momento”. Luiz F. Filho
“Não há coisa mais importante no mundo que a Salvação em Cristo… A Vida Eterna!”. Danny
“Camarão que dorme a onda leva!”. Alexandre Lyrio
“Gostaria de viver em um mundo onde os ricos não sejam tão ricos a ponto de comprar os pobres e os pobres não tão pobres a ponto de aceitar as propostas”. Lúcio Barbosa
“Vista do alto, a terra é, senão uma bola azul sempre a girar”. Danny
“Se nosso cérebro fosse tão simples a ponto de entendermos toda sua complexidade. Nós seríamos tão idiotas que não o entenderíamos”. Rodrigo Lima
“Eu amo a vida, se um dia eu parar de viver eu morro!”. Jaqueline C. Oliveira
“Estou vivo, mas sem Cristo não existo!”. Danny
“Daqui a vinte anos, você estará mais desapontado com as coisas que você deixou de fazer do que pelos erros que cometeu”. Raul Seixas
“Na busca desesperada de ter, o homem esquece de ser”. Gustavo de Assis
François Auguste René Rodin 1840-1917

François Auguste René Rodin (Paris, 12 de novembro de 1840 — Meudon, 17 de novembro de 1917), mais conhecido como François Auguste René Rodin, foi um escultor francês. Apesar de ser geralmente considerado o progenitor da escultura moderna, não se propôs a rebelar-se contra o passado. Foi educado tradicionalmente, teve o artesanato como abordagem em seu trabalho, e desejava o reconhecimento acadêmico, embora nunca tenha sido aceito na principal escola de arte de Paris.
Esculturalmente, Rodin possuía uma capacidade única em modelar uma superfície complexa, turbulenta, profundamente embolsa em argila. Muitas de suas esculturas mais notáveis foram duramente criticadas durante sua vida. Eles entraram em confronto com a tradição da escultura da figura predominante, onde as obras eram decorativas, estereotipadas ou altamente temáticas. Seu trabalho mais original partiu de temas tradicionais da mitologia e da alegoria, modelando o corpo humano com realismo e celebrando o caráter individual e fisicalidade. Rodin era sensível à controvérsias em torno de seu trabalho, mas se recusou a mudar seu estilo. Sucessivas obras trouxeram aumentos de favores do governo e da comunidade artística.
Do inesperado realismo de sua primeira grande figura – inspirada por sua viagem à Itália, em 1875 – para os memoriais não convencionais cujas comissões mais tarde ele procurou, sua reputação cresceu, de tal forma que se tornou o escultor francês proeminente de seu tempo. Em 1900, ele era um artista de renome mundial. Clientes particulares ricos procuraram seus trabalhos após sua mostra na Exposição Universal, e ele fez companhia com uma variedade de intelectuais e artistas de alto nível. Ele se casou com sua companheira ao longo da vida, Rose Beuret, no último ano de vida de ambos. Suas esculturas sofreram um declínio de popularidade após a sua morte em 1917, mas dentro de algumas décadas, o seu legado se solidificou. Rodin continua a ser um dos poucos escultores conhecidos fora da comunidade das artes visuais.
Biografia
Rodin nasceu em 1840 em uma família de classe operária de Paris, era o segundo filho de Marie Cheffer e Jean Baptiste Rodin, que era um funcionário do departamento de polícia. Foi em grande parte autodidata, começou a desenhar aos dez anos. Entre os 14 e 17 anos de idade, Rodin estudou na Petite École, uma escola especializada em arte e matemática, onde estudou desenho e pintura. Seu professor de desenho, Horace Lecoq de Boisbaudran, acreditava em primeiro desenvolver a personalidade de seus alunos para que eles observassem com seus próprios olhos e desenhassem a partir de suas lembranças. Rodin ainda agradeceu seu professor mais tarde em sua vida. Foi na Petite École que ele conheceu Jules Dalou e Alphonse Legros.

Em 1857, Rodin apresentou um modelo de argila de um companheiro para a Grand École em uma tentativa de ganhar uma entrada; ele não teve sucesso, e dois outros pedidos também foram negados. Dado que os requisitos de entrada na Grand École não eram particularmente elevados, as rejeições tornaram-se retrocessos consideráveis. Sua incapacidade em ganhar a vaga pode ter sido devida ao gosto neoclássico dos juízes, enquanto Rodin tinha sido educado em luz, a escultura do século XVIII. Deixando a Petite École em 1857, Rodin ganhava a vida como artesão e com ornamentos durante a maior parte das próximas duas décadas, a produção de objetos decorativos e enfeites arquitetônicos.
Sua irmã Maria, dois anos mais velha, morreu de peritonite em um convento em 1862. Seu irmão estava angustiado, e sentiu-se culpado por ter introduzido Maria a um pretendente infiel. Afastando-se da arte, Rodin juntou-se brevemente a uma ordem católica, a Congregação do Santíssimo Sacramento. Sendo São Pedro Julião Eymard fundador e chefe da congregação reconheceu o talento de Rodin e, sentindo sua falta de aptidão à ordem, o incentivou a continuar com sua escultura. Ele voltou a trabalhar como decorador, tendo aulas com o escultor de animais Antoine-Louis Barye. A atenção do professor ao detalhe – sua musculatura finamente tomada de animais em movimento – o influenciou significativamente.

Em 1864, Rodin começou a viver com uma jovem costureira chamada Rose Beuret, com quem ficaria – com variando compromisso – para o resto de sua vida. O casal teve um filho, Auguste Eugène Beuret (1866-1934). Naquele ano, Rodin ofereceu a sua primeira escultura à exposição, e entrou no estúdio de Albert Ernest Carrier Belleuse, um produtor em massa bem sucedida de objets d’art. Rodin trabalhou como assistente chefe de Carrier Belleuse até 1870, projetando decorações de telhado e escadas da entrada e enfeites. Com a chegada da Guerra franco-prussiana, Rodin foi chamado para servir na Guarda Nacional, mas o serviço foi breve devido à sua miopia. O trabalho dos decoradores tinha diminuído por causa da guerra, Rodin ainda necessitava sustentar sua família; a pobreza era uma de suas dificuldades constantes até cerca dos 30 anos de idade. Carrier Belleuse logo pediu a Rodin que o acompanha-se na Bélgica, onde eles iriam trabalhar em ornamentação para a bolsa de Bruxelas.
Rodin planejou ficar na Bélgica por alguns meses, mas ele passou os próximos seis anos fora da França. Foi um momento crucial em sua vida. Havia adquirido habilidade e experiência como artesão, mas ninguém tinha visto ainda sua arte, que estava sentada em sua oficina, já que ele não podia pagar a fundição. Embora seu relacionamento com Carrier Belleuse tenha deteriorado, Rodin encontrou outro emprego em Bruxelas, exibindo algumas obras em salões de beleza, e sua companheira Rose logo se juntou a ele lá. Tendo guardado dinheiro suficiente para viajar, Rodin visitou a Itália por dois meses em 1875, onde ele foi atraído pela obra de Donatello e Michelangelo. Seu trabalho teve um efeito profundo em sua direção artística. Rodin disse: “É Michelangelo, que me libertou da escultura acadêmica.” Voltando a Bélgica, ele começou a trabalhar em A Idade do Bronze, uma figura masculina em tamanho natural, cujo realismo trouxe atenção a Rodin, mas levou a acusações de fraude.
Independência Artística

Rose Beuret e Rodin retornaram a Paris em 1877, movendo-se para um pequeno apartamento na Margem Esquerda. O infortúnio cercou sua vida: sua mãe, que queria ver seu filho se casar, estava morta, e seu pai que era cego e senil era cuidado por sua cunhada, Aunt Thérès. Seu filho Auguste, de onze anos de idade, possivelmente com atraso de desenvolvimento, também estava no sempre útil cuidado de Thérès. Rodin tinha abandonado, essencialmente, seu filho por seis anos, e gostaria de ter uma relação muito limitada com ele ao longo de sua vida. Pai e filho agora se juntaram ao casal em seu apartamento, com Rose como cuidadora. As acusações de falsidade que cercam A Idade do Bronze continuaram. Rodin procurou cada vez mais a companhia feminina mais suave, em Paris, e Rose ficou em segundo plano.
Ganhava a vida colaborando com escultores mais estabelecidos em comissões públicas, principalmente memoriais e peças arquitetônicas neo-barrocas no estilo de Carpeaux. Em competições de comissões apresentou modelos de Denis Diderot, Jean Jacques Rousseau, e Lazare Carnot, todos sem sucesso. Em seu próprio tempo, trabalhou em estudos para a criação de seu próximo trabalho importante, São João Batista Pregando.
Em 1880, Carrier Belleuse – agora diretor de arte da fábrica nacional de porcelana de Sèvres – lhe ofereceu uma posição de meio período como designer. A oferta foi, em parte, um gesto de reconciliação, e Rodin aceitou. Essa sua parte, que apreciava os gostos do século XVIII foi despertada, e ele mergulhou em projetos de vasos e enfeites de mesa que trouxeram fama à fábrica em toda a Europa.

A comunidade artística apreciou seu trabalho nesse sentido, e Rodin foi convidado para o Salon de Paris por seus amigos como o escritor Léon Cladel. Durante suas primeiras aparições nesses eventos sociais, parecia tímido; em seus últimos anos, como sua fama cresceu, ele mostrou a loquacidade e temperamento pelo qual se tornou mais conhecido. O estadista francês Léon Gambetta expressou seu desejo em conhecê-lo, e o escultor o impressionou quando eles se encontraram em um salão. Gambetta falou de Rodin, em vez de vários ministros do governo, provavelmente incluindo Edmund Turquet, o subsecretário do Ministério de Belas Artes, a quem, eventualmente, o conheceu.
Suas obras mais célebres, O Beijo, que faz parte de uma série de esculturas realizadas para a Porta do Inferno, do Museu de Artes Decorativas, O Pensador, da mesma série, e o retrato de Balzac confirmam isso. Há um museu em Paris dedicado às suas obras e vida, o Musée Rodin), situado no Hôtel Biron, ao lado do Hôtel des Invalides, monumento onde se encontra o túmulo de Napoleão.
Rodin teve como assistente a escultora Camille Claudel, com quem teve um romance e cujos trabalhos são muitas vezes confundidos com os de Rodin. Camille acreditava que Rodin queria se apropriar dos seus trabalhos. À época, foi considerada insana e terminou seus dias internada em um manicômio.
Rodin conquistou fama em vida, e suas obras chegaram a ser as mais apreciadas no mercado de arte europeu e americano. Hoje em dia encontram-se nos museus mais importantes do mundo.
Faleceu em 17 de novembro de 1917. Encontra-se sepultado no Museu Rodin, Meudon, Ilha de França, Paris na França.
Charles Darwin 1809-1872
Um pouco de sua história

Nasceu no dia 12 de fevereiro de 1809, na cidade de Shrewsburry, Inglaterra.
Quando criança cultivava o hábito de colecionar besouros e acabou ficando obcecado por isso. Seu pai temia que não seria capaz de fazer nada além de caçar ratos e besouros e que acabasse por desgraçar o nome da família. Por ser um hábil caçador, aprendeu a observar o hábito dos animais. Concluiu que o prazer de observar era maior do que o prazer de caçar.
Ingressou no curso de medicina seguindo os passos do pai e do avô. No entanto, desde que teve de operar um doente sem anestesia, descobriu que não daria para isso e abandonou o curso. Seu pai deixou propriedades a ponto de não precisar trabalhar para seu sustento.
Aconselhou-o para que se dedicasse à Igreja Anglicana e ele o fez em 1827. Mas não ficou feliz com o que aprendeu lá. Por exemplo: segundo o que o próprio Darwin contou, ensinavam que a terra foi criada às 9h do dia 23 de outubro de 4004 a.C. e que todas as espécies foram criadas ao longo de 6 dias e que jamais teriam sofrido mudanças desde então.
Charles desenvolveu sua paixão pela natureza.

Seu professor J.S. Henslow o recomendou para a tripulação do Beagle, onde a tarefa do capitão era mapear mares e costas desconhecidas pela Marinha Britânica. A viagem durou 5 anos. Foi incorporado como naturalista apesar de não ter qualificação acadêmica para isso. Mas seu dever acabou sendo fazer companhia ao capitão altamente autoritário. Ele cumpriu fielmente sua função e aproveitou durante as paradas para coletar tudo o que pudesse: rochas, fósseis, aves, insetos e animais grandes que ele mesmo empalhava. Em cada porto enviava seu material para Henslow na Inglaterra. E durante essa viagem escreveu um diário.
Na volta, que se deu no dia 02 de outubro de 1836, estava convencido de que as espécies animais sofrem mudanças. Porém, não sabia como isso ocorria. Junto de Richard Owen, classificou o material coletado e publicou “Zoologia da Viagem do Beagle”.
Casou-se com Ema e teve 10 filhos, no que pareceu, foi um casamento feliz.

Um livro despertou seu interesse, de Thomas Malthus, afirmava que as populações tendem a crescer geometricamente a menos que sejam impedidas. Aí estava sua resposta. Eram as alterações que permitiam que um indivíduo prosperasse, enquanto os outros que não sofriam essas alterações, pereciam. Fez uma alteração fundamental na teoria de Lamarck utilizando os exemplos das girafas.
Nela, Lamarck afirmava que as girafas iam ficando com o pescoço comprido pela necessidade de se alcançar os galhos mais altos das árvores. Porém a mudança fundamental introduzida por Darwin é que: as girafas não iam esticando o pescoço e sim, apenas as de pescoço comprido sobreviveriam.

Ele chegou a publicar um ano antes a obra “A Transmutação das Espécies” onde falava dessas mudanças, mas não arriscou explicá-las.
A sua principal obra “Sobre a Origem das Espécies por meio da Seleção Natural” só foi publicada 20 depois de sua viagem, quando recebeu uma carta de outro naturalista inglês, Alfred Russel Wallace que fez observações e chegou as mesmas conclusões.
Foram 1250 exemplares de 502 páginas que esgotaram num único dia, 24 de novembro de 1859.
Todo o cuidado que teve para não usar a palavra “evolução” não adiantou pois suas teorias fizeram desabar as teorias da igreja sobre a criação do mundo. Foram anos de debates ferozes, onde uns dos principais adversários foram: Richard Owen, o bispo de Oxford, Samuel Wilberforce e o escritor Edmung Gosse. Seus defensores foram o geólogo Charles Lyell, o botânico Joseph Hooker e o zoólogo Thomas Henry Ruxley. Nestes debates, Charles pouco apareceu.
Charles Darwin deixou uma obra extensa. Guardava em seu escritório frascos com amostras de várias espécies animais e vegetais. e apesar da igreja fazer campanhas severas contra as suas idéias, permitiu que, após sua morte em 19 de abril de 1872, fosse enterrado na abadia de Westminster, ao lado de Isaac Newton. Esse fato fez com que, um tempo depois do enterro, seu filho fizesse um comentário: “Você pode imaginar que conversas deliciosas o pai e Sir Isaac terão à noite, depois que a abadia fechar e tudo ficar quieto?”
Johann Carl Friedrich Gauss 1777-1855
Carl Friedrich Gauss nasceu em 30 de abril de 1777 na cidade de Brunswick, hoje Alemanha. Trabalhou em diversos campos da matemática e da física dentre eles a teoria dos números, geometria diferencial, magnetismo, astronomia e ótica. Seu trabalho influenciou imensamente outras áreas. Aos sete anos de idade, Carl Friedrich começou a escola primária, e seu potencial foi notado quase imediatamente. Seu professor, Büttner, e seu assistente, Martin Bartels, ficaram pasmos quando Gauss somou os inteiros de 1 a 100 imediatamente, declarando que a soma era 50 pares de números, cada par somando 101.
Em 1788 Gauss começou o curso ginasial, com a ajuda de Büttner e Bartels com quem aprendeu alto alemão e latim. Depois de receber um estipêndio do Duque de Brunswick – Wolfenbüttel, em 1972, Gauss entrou em Brunswick Collegium Carolinum. Na academia, Gauss descobriu a lei do pressagio, o teorema de binômio e a aritmética – geometria fundamental, como também a lei de reciprocidade quadrática e o teorema de número primo. Em 1795 Gauss deixou Brunswick para estudar na Universidade de Göttingen.
Seu único amigo entre os estudante, durante anos, foi Farkas Bolyai. Gauss deixou Göttingen em 1798 sem um diploma, no entanto, antes realizou uma de suas mais importantes descobertas – a construção de umorreum polígono regular de 17 faces unicamente com régua e compasso. Este era o principal avanço neste campo desde o tempo de matemática grega e foi publicado como Seção VII do famoso trabalho de Gauss, Disquisitiones Arithmeticae, publicado em 1801. Gauss retornou a Brunswick em 1799 onde recebeu seu grau. O Duque de Brunswick tinha concordado em continuar o estipêndio de Gauss, e lhe pediu uma dissertação doutoral para a Universidade de Helmstedt. Gauss conhecia Pfaff que foi escolhido ser seu aconselhador e o ajudou na confecção da discussão do teorema fundamental de álgebra.
Em junho de 1801, Zach, um astrônomo, publicou as posições de orbital de Ceres, um novo planeta que foi descoberto por G Piazzi, um astrônomo italiano no dia 1 janeiro de 1801. Infelizmente, Piazzi só tinha podido observado 9 graus de sua órbita antes de desaparecesse atrás do Sol. Zach publicou diversas predições de suas posições, incluindo uma deferida por Gauss. Ceres foi redescoberto por Zach no dia 7 de dezembro de 1801, data quase exata onde Gauss predisse. Embora ele não descobriu seus métodos na ocasião, Gauss tinha usado o seu próprio método de aproximação de quadrados. Em junho de 1802 Gauss visitou Olbers o qual em março daquele ano, descobriu Pallas e Gauss investigou sua órbita. Olbers pediu para que Gauss fosse eleito o diretor do novo observatório proposto em Göttingen, mas nenhuma medida foi tomada. Gauss começou a se corresponder com Bessel porém não voltou a encontrá-lo até o ano de 1825.
Gauss casou-se com Johanna Ostoff no dia 9 de outubro de 1805. Apesar de ter uma vida pessoal feliz pela primeira vez, seu benfeitor, o Duque de Brunswick, foi morto lutando para o exército prussiano. Em 1807 Gauss deixou Brunswick para assumir a posição de diretor do observatório de Göttingen. Em 1808 seu pai vem a falecer e, um ano depois, sua esposa, que acabara de dar a luz a seu segundo filho, também morre. Gauss casou-se novamente no ano seguinte com Minna, a melhor amiga Johanna e, apesar de terem tidos três filhos, este matrimônio parecia ser uma conveniência de Gauss.

O trabalho de Gauss nunca parecia sofrer com sua tragédia pessoal. Publicou seu segundo livro, Theoria motus corporum coelestium em conicis de sectionibus ambientium de Solem, em 1809, o principal material sobre movimento de corpos celestiais, dividido em dois volumes. No primeiro volume ele discutiu equações diferencial, seções cônicas e órbitas elípticas, enquanto no segundo, a parte principal do trabalho, ele mostrou como calcular e então refinar a estimação da órbita de um planeta. As contribuições de Gauss para astronomia cessam a partir de 1817, apesar de ter feito observações até os 70 anos.
A maior parte do tempo de Gauss era gasto em um novo observatório, finalizado em 1816, porém ainda achara tempo para se dedicar a outros assuntos. As publicações realizadas por ele durante esse período incluem Disquisitiones generales circa seriem infinitam, um tratamento rigoroso de série e uma introdução da função hipergeometrica, Methodus nova integralium valores per approximationem inveniendi, Bestimmung der Genauigkeit der Beobachtungen, uma discussão sobre estatísticas estimadas, e Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodus nova tractata. Seu trabalho posterior foi inspirado por problemas geodésicos e estava principalmente preocupado com a teoria potencial.
Na realidade, em 1820, Gauss se achou cada vez mais interessado em geodésia, ciência que se ocupa da forma e da grandeza da terra ou de uma parte de sua superfície. Gauss, em 1818 recebeu a oportunidade do projeto geodésico do estado de Hanover e ficou grato em aceitá-lo e se encarregou da pesquisa. Fazia medidas durante o dia e as calculada durante à noite, usando sua extraordinária capacidade mental por cálculos . Escrevia regularmente a Schumacher, Olbers e Bessel, relatando seus progressos e discutindo os problemas. Por causa de suas pesquisas, Gauss inventou o heliotrópio que trabalhava refletindo os raios do Sol usando u e um pequeno telescópio pequeno. Porém, linhas básicas inexatas eram usadas para a pesquisa e uma rede não satisfatória de triângulos. Gauss desejou constantemente que lhe tivessem aconselhado a procurar alguma outra ocupação mas, apesar disso, ele publicou mais de 70 documentos entre 1820 e 1830.

Em 1822 Gauss ganhou o Prêmio da Universidade de Copenhague Theoria attractionis… junto com a ideia de traçar uma superfície sobre outra de forma que as duas sejam semehantesr nas partes menores. Este documento foi publicado em 1825 e conduziu a muitas publicações posteriores. O documento Theoria combinationis observationum erroribus minimis obnoxiae (1823), com seu suplemento (1828), foi dedicado a estatísticas matemáticas, em particular para o método dos quadrados.
No início de 1800 Gauss teve seu interesse voltado a possível existência de uma geometria não-Euclidiana. Discutiu este tópico com Farkas Bolyai e, por correspondência, com Gerling e Schumacher. Em uma revisão de um livro em 1816 ele discutiu provas das quais deduziram o axioma comparando-os com os axiomas Euclidianos, sugerindo que acreditassem na existência de uma geometria não-Euclidiana, embora isso ainda fosse bastante vago. Gauss confidenciou seus estudos a Schumacher, acreditando que, se admitisse em público a existência de tal geometria, sua reputação poderia ser abalada.
Em 1831 Farkas Bolyai enviou a Gauss o trabalho de seu filho János Bolyai sobre o assunto. Gauss respondeu: Exaltar isto poderia significar exaltar a mim mesmo Uma década depois, quando ele estava informado do trabalho de Lobachevsky sobre o assunto, elogiou seu caráter “genuinamente geométrico”, enquanto em uma carta para Schumacher em 1846, relatou que ele havia tido as mesmas convicções durante 54 anos, indicando que já sabia da existência de uma geometria não-Euclidiana desde os 15 anos de idade. Gauss teve seu principal interesse voltado para a geometria diferencial, e publicou muitos documentos sobre o assunto. Disquisitiones generales circa superficies curva (1828) era seu trabalho mais renomado neste campo. Na realidade, este documento subiu aos seus interesses geodésicos, mas conteve tais ideias geométricas como curvatura de Gauss. O papel também inclui o Teorema egregrium de Gauss: Se uma área em E³ pode ser desenvolvida (i.e. isometricamente traçado) em outra área de E³ os valores das curvaturas de Gauss são idênticos em pontos correspondentes.
O período de 1817-1832 foi particularmente infeliz para Gauss. Teve sua mãe doente em 1817, e ficou com ela até sua morte, em 1839. enquanto argumentava com sua esposa e a família dela se eles deveriam se mudar para Berlim pois tinha lhe oferecido uma vaga na Universidade de Berlim. Porém como Gauss não gostava de se mudar, acabou por ficar em Göttingen. Em 1831 morre a segunda esposa de Gauss, após uma longa doença. Em 1831, Wilhelm Weber chegou a Göttingen para preencher a cadeira de Tobias Mayer como professor de física. Gauss tinha trabalhado em física até 1831, publicando Uber ein neues allgemeines Grundgesetz der Mechanik e Principia generalia theoriae figurae fluidorum em aequilibrii de statu que discutia as forças de atração. Estes documentos estavam baseado na teoria de potencial de Gauss que provou de grande importância de seu trabalho na física e depois ele veio a acreditar no potencial de sua teoria e o método dos quadrados provinham ligações vitais entre a ciência e natureza. Em 1832, Gauss e Weber começaram a investigar a teoria de magnetismo terrestre depois de Alexander von Humboldt ter tentado obter ajuda de Gauss para fazer um grid de pontos de observação magnética ao redor da Terra.
Gauss estava entusiasmado por este projeto e, antes de 1840, já tinha escrito três importantes documentos sobre o assunto: Intensitas vis magneticae terrestris ad mensuram absolutam revocata (1832), Allgemeine Theorie des Erdmagnetismus (1839) e Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskräfte (1840). Estes documentos que tratavam das teorias atuais sobre o magnetismo terrestre, incluindo as idéias de Poisson, medida absoluta das força magnética e uma definição empírica de magnetismo terrestre.

A Allgemeine Theorie mostrou que só pode haver dois pólos no globo o que pode provar um importante teorema sobre a intensidade da componente horizontal da força magnética junto com o ângulo de inclinação. Gauss usou a equação de Laplace para ajudá-lo com cálculos, e acabou especificando um local para o pólo sul magnético. Humboldt inventara um calendário para observações de declinação magnética. Porém, assim que o novo observatório magnético que de Gauss ficou concluído (isso se consumou em 1833 – livre de todos os metais magnéticos). ele se pôs em alterar muitos dos procedimentos de Humboldt, o que não lhe agradou muito. Porém, as mudanças de Gauss obtiveram resultados mais precisos com menos esforço. Gauss e Weber alcançaram muitos no seis anos em que tiveram juntos.
Eles descobriram as leis de Kirchhoff, como também construíram um primitivo dispositivo de telégrafo que poderia enviar mensagens até uma distância de 5000 pés. Porém, este foi apenas um passatempo agradável para Gauss. Ele estava mais interessado na tarefa de estabelecer uma rede mundial de pontos de observação magnética. Esta ocupação produziu muitos resultados concretos. Foram fundados o Magnetischer Verein e seu jornal, e o atlas geomagnético foi publicado. Os resultados de Gauss e Weber eram publicados no próprio jornal periódico de Weber durante o período de 1836 a 1841.
Em 1837, Weber foi forçado a deixar Göttingen quando foi envolvido em uma disputa política e, neste período, diminuíram gradualmente as atividade de Gauss. Ele ainda escreveu cartas a respeito às descobertas de cientistas da mesma categoria que normalmente observam que ele tinha conhecido os métodos por anos mas nunca tinha sentido a necessidade de publicá-los. Às vezes ele parecia extremamente agradado com avanços feitos por outros matemáticos, particularmente o de Einstein e de Lobachevsky. Gauss passou os anos de 1845 a 1851 atualizando os fundos monetários da Universidade de Göttingen. Este trabalho lhe deu uma experiência em práticas financeiras, com isso, Gauss fez sua fortuna através de investimentos astutos em companhias privadas. Dois dos últimos estudantes doutorais de Gauss, Precentor de Moritz e Dedekind. Dedekind escreveram uma descrição sobre seu supervisor: … normalmente ele se sentava de modo confortável, olhando para baixo, ligeiramente se inclinou, com mãos dobradas sobre seu o colo dele. Ele falou bastante livremente, muito claramente, simplesmente e claramente: mas quando ele quis enfatizar um ponto de vista novo… então ele ergueu a cabeça dele, virada a um desses se sentando próximo a ele, e contemplou a ele com o bonito dele, penetrando olhos azuis durante a fala enfática. … Se ele procedesse de uma explicação de princípios ao desenvolvimento de fórmulas matemáticas, então ele se levantou, e em uma postura muito vertical imponente ele escreveu em um quadro-negro ao lado dele dentro o dele peculiarmente letra bonita: ele sempre teve sucesso por economia e arranjo deliberado dentro sobreviva com um espaço bastante pequeno. Em de quem conclusão cuidadosa ele colocou valor especial para exemplos numéricos, ele trouxe os dados requeridos em pouco desliza de papel. Gauss apresentou a conferência de jubileu dourada dele em 1849, cinquenta anos depois que o diploma dele tivesse sido concedido através de Universidade de Hemstedt. Era adequadamente uma variação na dissertação dele de 1799.
Da comunidade matemática só Jacobi e Dirichlet estavam presentes, mas Gauss recebeu muitas mensagens e honours. De 1850 onwards o trabalho de Gauss era novamente de quase tudo de uma natureza prática embora ele aprovou a tese doutoral de Riemann e ouviu a conferência probatória dele. A última troca científica conhecida dele estava com Gerling. Ele discutiu um pêndulo de Foucalt modificado em 1854. Ele também pôde assistir à abertura da ligação de estrada de ferro nova entre Hanover e Göttingen, mas isto provou ser a última excursão dele.
Friedrich Gauss morreu de manhã cedo, durante seu sono em 23 fevereiro, 1855 em Göttingen, Hanover, hoje Alemanha)
Arquimedes 287 a.C. – 212 a.C.

Arquimedes, filho do astrônomo Fídeas, era nativo de Siracusa, na Sicília. Há relatos de sua visita ao Egito, onde inventou um sistema de bombeamento chamado Parafuso de Arquimedes, em uso ainda hoje.
Há indícios muito fortes de que em sua juventude, Arquimedes tenha estudado com os sucessores de Euclides, em Alexandria. Com certeza ele era completamente familiarizado com a Matemática lá desenvolvida, conhecendo pessoalmente os matemáticos daquela região. Ele mesmo mandava alguns de seus resultados para Alexandria com mensagens pessoais.

No prefácio de Sobre espirais Arquimedes nos conta uma história curiosa acerca de seus amigos em Alexandria. Ele tinha o hábito de mandar o texto de seus últimos teoremas, mas sem as demonstrações. Aparentemente alguém em Alexandria estava roubando os resultados de Arquimedes e afirmando que eram seus. Na última vez que fez isso, enviou dois resultados falsos.
…aqueles que afirmam descobrir tudo, mas não produzem provas de suas afirmações, podem estar enganados fingindo descobrir o impossível.
De fato, existem inúmeras referências a Arquimedes nos escritos de sua época, dada a reputação quase sem par que ele ganhou neste período. Curiosamente a razão para isso não era um interesse generalizado em Matemática, mas sim nas máquinas que inventou para serem usadas na guerra. Estas armas foram particularmente eficientes na defesa de Siracusa contra os Romanos, liderados por Marcelo.
Escreve Plutarco
…quando Arquimedes começou a manejar suas máquinas, ele de uma só vez atirou contra as forças terrestres todos os tipos de mísseis, e imensas massas de rocha que caíram com barulho e violência inacreditáveis, contra as quais nenhum homem poderia resistir em pé.
Outras invenções de Arquimedes, como a polia composta, também colaboraram para que sua fama se perpetuasse. Novamente citando Plutarco:
[Arquimedes] afirmou [em uma carta ao Rei Hierão] que, dada uma força, qualquer peso poderia ser movido, e até mesmo se gabando, disse que se houvesse outra Terra, esta poderia ser movida. Hierão maravilhou-se com isto e pediu uma demonstração prática. Arquimedes tomou um dos navios da frota do rei – que não podia ser movido a não ser por muitos homens – carregou-o com muitos passageiros e lotou-o de carga. Arquimedes colocou-se a distância e puxou as polias, movendo o navio em linha reta suavemente, como se estivesse no mar.

Mesmo tendo Arquimedes obtido fama por suas invenções mecânicas, ele acreditava que a Matemática em sua forma mais pura era a única coisa que valia a pena.
As conquistas de Arquimedes são de tirar o fôlego. Ele é considerado por muitos historiadores como um dos maiores matemáticos de todos os tempos. Ele chegou a aperfeiçoar um método de integração que permitia calcular áreas, volumes e áreas de superfícies de muitos corpos.
Arquimedes foi capaz de aplicar o método da exaustão, que é uma forma primitiva de integração, para obter uma vasta gama de resultados importantes, alguns dos quais chegaram até os dias de hoje.
* O tratado Sobre equilíbrios planos aborda os princípios fundamentais da mecânica, usando métodos geométricos. Arquimedes descobriu teoremas fundamentais a respeito do centro de gravidade de figuras planas, todos constantes deste trabalho. Em particular ele encontra, no livro 1, o centro de gravidade do paralelogramo, do triângulo e do trapézio.
* O livro 2 é inteiramente devotado a encontrar o centro de gravidade de um segmento de parábola. Na Quadratura da parábola Arquimedes encontra a área de um segmento de parábola formado pelo corte de uma corda qualquer.
* No primeiro volume de Sobre a esfera e o cilindro Arquimedes mostra que a superfície de uma esfera é quatro vezes a do grande círculo, acha a área de qualquer segmento da esfera, mostra que o volume de uma esfera é dois terços do volume do cilindro circunscrito, e que a superfície da esfera é dois terços da superfície do cilindro circunscrito, incluindo-se as bases.
* Em Sobre espirais Arquimedes define uma espiral e estabelece as propriedades fundamentais relacionando o comprimento do vetor raio com os ângulos de revolução que geram as espirais. Ele também apresenta resultados sobre tangentes às espirais, bem como demonstra como calcular áreas de partes da espiral.
* Em Sobre conóides e esferóides Arquimedes examina os parabolóides de revolução, hiperbolóides de revolução e esferóides obtidos pela rotação de uma elipse em torno de um de seus eixos.
* Sobre corpos flutuantes é o trabalho onde Arquimedes estabelece os princípios básicos da Hidrostática. Seu teorema mais famoso – que dá o peso de um corpo imerso em um líquido – chamado Princípio de Arquimedes, consta deste trabalho.
* Em Medidas do círculo Arquimedes mostra que o valor exato de “pi” situa-se entre 310/71 e 31/7. Ele obteve este resultado circunscrevendo e inscrevendo um círculo com polígonos regulares com 96 lados!

Um problema preocupava Hierão, tirano de Siracusa, no século III a.C.: havia encomendado uma coroa de ouro, para homenagear uma divindade, mas suspeitava que o ourives o enganara, não utilizando ouro maciço em sua confecção. Como descobrir, sem danificar o objeto, se seu interior continha uma parte feita de prata? Só um homem talvez conseguisse resolver a questão: seu amigo Arquimedes, famoso matemático e inventor de vários engenhos mecânicos. Hierão mandou chamá-lo e pediu-lhe urna resposta que pusesse fim à sua dúvida. Arquimedes aceitou a incumbência e pôs-se a procurar a solução para o problema. Esta lhe ocorreu durante o banho. Observou que a quantidade de água que se elevava na banheira, ao submergir, era equivalente ao volume de seu próprio corpo. Ali estava a chave para resolver a questão proposta pelo tirano. No entusiasmo da descoberta, Arquimedes saiu nu pelas ruas, gritando: Eureka! Eureka! (“Achei! Achei!”).
Agora, bastava aplicar o método que descobrira. Mediu então a quantidade de água que transbordava de um recipiente cheio, quando nele mergulhava, sucessivamente, o volume de um peso de ouro igual ao da coroa, o volume de um peso de prata igual ao da coroa e o volume da própria coroa. Este, sendo intermediário aos outros dois, permitia determinar a proporção de prata que fora misturada ao ouro.

Essa passagem parece ser uma das muitas lendas que, desde a Antiguidade, envolveram a vida de Arquimedes. Na verdade, para resolver um problema daquele tipo, relativo à determinação do peso específico de um metal, ele precisava apenas aplicar o princípio que rege o fenômeno do empuxo (força vertical que empurra para cima um corpo imerso em um fluido). Esse princípio – que explica porque um navio flutua na água e porque um aeróstato sobe no ar – foi estabelecido por Arquimedes nos seus dois livros, Sobre os corpos flutuantes, com os quais inaugurou um novo ramo da ciência física: a hidrostática. No primeiro daqueles dois livros, ele enuncia o princípio que se tornou conhecido como “princípio de Arquimedes”: “Um sólido mais pesado que o fluido em que está imerso vai para o fundo do fluido, e se é pesado dentro do fluido ele será mais leve que seu verdadeiro peso, de um peso igual ao fluido deslocado”.
Entretanto, essa conclusão não era, de modo algum, fruto de um súbito “estalo”. Representava o coroamento de uma longa tradição científica que, desde o século VI a.C., desenvolvera as pesquisas matemáticas e buscava uma explicação racional para os diferentes fenômenos observados. A glória de Arquimedes consistiu, porém, em não apenas fazer avançar as matemáticas abstratas – ampliando as conquistas dos grandes matemáticos do passado, como Pitágoras, Tales, Árquitas de Tarento, Eudoxo e Euclides -, mas em ser igualmente um grande físico, engenheiro e técnico genial: inventava e fabricava aparelhos destinados às suas próprias pesquisas, e criava inclusive máquinas de guerra temíveis por sua eficácia. Representando o apogeu da ciência grega, é considerado o precursor do método experimental nas ciências fisico-matemáticas.
Filho do astrônomo Fídias, Arquimedes nasceu em 287 a.C., em Siracusa, na Sicília, que então fazia parte da Grécia ocidental ou Magna Grécia. Embora os dados fantasiosos permeiem todos os informes sobre sua vida, parece certo que estudou em Alexandria (Egito), um dos grandes centros culturais da época. Ali teria conhecido Euclides, já velho, e seus discípulos imediatos; e o matemático Canon de Samos, de quem se tornou amigo. Não é certo, porém, que ali tivesse criado o chamado “parafuso de Arquimedes”, empregado para retirar água das minas do Egito. Na verdade, esse aparelho já existia, ao que parece, há bastante tempo, sendo utilizado para tirar água do Nilo.

Reduzindo o equilíbrio de forças a um simples problema geométrico, estudou o equilíbrio dos sólidos, o funcionamento da alavanca e o movimento dos corpos celestes, além de ter organizado uma coleção – a mais completa da Antiguidade – de figuras planas com os centros de gravidade perfeitamente localizados. Além disso, também procurava utilidades práticas para suas descobertas. Extraordinário engenheiro, construiu, segundo depoimento de Cícero (106 – 43 a.C.), um planetário que reproduzia os diferentes movimentos dos corpos celestes; e um aparelho para medir as variações do diâmetro aparente do Sol e da Lua, um protótipo do modelo, mais requintado, que será construído pelo astrônomo Hiparco, no século II a.C.

Atribui-se ainda a Arquimedes a idealização dos célebres “espelhos ustórios” (ustório = que queima, que facilita a combustão), espelhos curvos com os quais os defensores de Siracusa teriam queimado a distância – pela concentração dos raios solares – os navios romanos que sitiavam a região. Se tal fato pertence ao lado lendário de sua biografia, parece entretanto não haver dúvida de que Arquimedes, depois de colaborar com seus engenhos bélicos para a defesa de sua cidade natal, foi morto durante o massacre que se seguiu à tomada de Siracusa pelo cônsul romano Marco Cláudio Marcelo, em 212 a.C. Atendendo a um pedido do sábio, foi colocada em seu túmulo uma coluna na qual fora gravado um cilindro circunscrito a uma esfera, para comemorar a maneira pela qual calculou a área de uma superfície esférica.
Segundo consta, Arquimedes teria dito a Hierão: “Deem-me um ponto de apoio e eu levantarei a Terra”. Não era a pretensão de se comparar ao mitológico e super humano Héracles – que os romanos chamarão de Hércules -, divindade símbolo da força. Era a certeza matematicamente garantida – de que o princípio da alavanca, que ele havia estabelecido, representava extraordinário recurso prático para a multiplicação de uma força.
Tradicionalmente, a geometria grega vinha investigando processos de transformação de figuras curvas em retas, equivalentes. A quadratura do círculo, por exemplo, constituía um problema que vários matemáticos procuraram resolver. Arquimedes dedicou-se profundamente a esse tipo de questão – e um dos seus principais livros sobre Matemática intitulou-se justamente Tratado da quadratura da parábola.
A transformação do curvilíneo em retilíneo é feita por Arquimedes através do chamado método “de exaustão”. Se um triângulo é inscrito num círculo, sua área é tão claramente menor que a do círculo quanto a do triângulo circunscrito é maior. No entanto – eis o procedimento adotado por Arquimedes – multiplicando-se o número de lados dessas figuras, as áreas dos polígonos formados, inscritos e circunscritos, já se aproximam mais da área do círculo. E com o multiplicar sucessivo dos lados, os polígonos assim formados apresentam áreas que crescem (para os inscritos) e diminuem (para os circunscritos), aproximando-se da do círculo, embora nunca coincidam com ela.

Arquimedes conseguiu ir multiplicando o número de lados dos polígonos até obter figuras de 96 lados; verificou que as áreas respectivas, apesar de cada vez mais próximas do círculo, eram sempre um pouco maiores ou um pouco menores. Havia aqui também um procedimento que subentendia a aproximação de um valor exato – a área do círculo; esta era um “limite” a ser atingido, uma “justa medida” que só permitia abordagens aproximadas.
O que estava implícito nesse método de resolução de um problema geométrico era – como no caso do estabelecimento do valor de “pi” – a existência de valores infinitesimais, que justificavam a gradativa variação de tamanhos e grandezas. Aqui também Arquimedes antecipa conquistas que a Matemática só efetivará plenamente no final do século XVII, com o cálculo infinitesimal de Leibniz e Newton.
A liberdade não era, porém, patrimônio de todos os gregos. Muitos eram escravos e, por isso, destituídos do direito de cidadania. O filósofo Aristóteles chega a afirmar que para alguns a escravidão era um fato natural e inerente à natureza dos indivíduos que, não possuindo certas capacidades. intelectuais de raciocínio abstrato (a “alma poética” para os gregos), deviam, como escravos, se ocupar apenas de atividades manuais.
Esse preconceito que, com raras exceções, era generalizado na sociedade escravista dos gregos, não poderia deixar de repercutir, além do campo propriamente político, no desenvolvimento da investigação científica e filosófica. O menosprezo pelas atividades manuais, exercidas por homens sem liberdade, foi certamente o fator decisivo para restringir a ciência grega ao nível quase exclusivamente teórico e para impedir o desenvolvimento da experimentação. A ciência deveria ser fruto do intelecto de homens livres e, portanto, capazes de especulação – e não o resultado de simples manipulações e experiências.

Poucos escaparam às limitações desse modo de pensar, que criava obstáculos à verificação empírica e bloqueava o campo das aplicações práticas dos conhecimentos teóricos. O próprio Arquimedes pagou tributo, ao que parece, a esse preconceito de natureza socioeconômica. Embora precursor do moderno método experimental, e apesar de ter sido o maior engenheiro da Antiguidade, também ele considerava como suprema realização da inteligência humana as verdades científicas abstratas – que as matemáticas formulavam plenamente. Conta Plutarco que, quando solicitado a escrever um manual de engenharia, Arquimedes se negou, alegando que “considerava o trabalho de engenheiro, assim como tudo o que dissesse respeito às necessidades da vida, como algo sem nobreza e vulgar”. Ele desejava que sua fama diante da posteridade fosse fundada inteiramente em sua contribuição à teoria pura. O que glorificou seu nome, entretanto, mais do que o cálculo de “PI” por aproximações sucessivas, foi o princípio fundamental da hidrostática, a que ele chegara pela mais simples observação da realidade.
Arquimedes foi morto em 212 A.C. durante a captura de Siracusa pelos Romanos na segunda guerra Púnica. Depois de todos os seus esforços para manter os romanos na baía com as suas máquinas de guerra, estes invadiram Siracusa, não impedido o estudioso de ficar refletindo sobre um problema geométrico que traçava na areia, não se apercebendo desta invasão. Apresentou-se lhe um soldado dando-lhe ordem de que o acompanhasse a casa de Marcelo, ele porém ignorou-o, irritando o soldado fazendo com que este o matasse com a sua espada.
Johannes Kepler 1571-1630
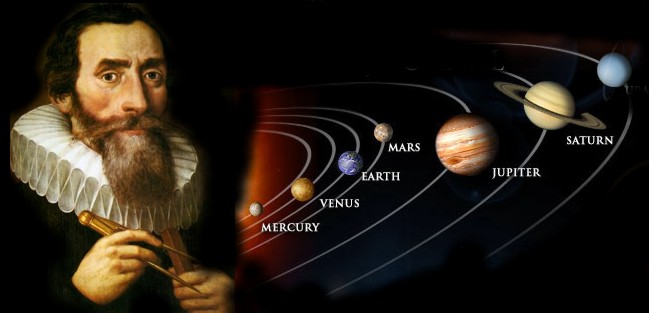
Os estudos Johannes Kepler nasceu em 27 de dezembro de 1571, no sul da atual Alemanha, que naquela época pertencia ao Sacro Império Romano, em uma cidade chamada Weil der Stadt, região da Swabia. Era filho de Heinrich Kepler, um soldado, e de sua esposa Katharina, cujo sobrenome de solteira era Guldenmann. Seu avô paterno, Sebald Kepler, era prefeito da cidade, apesar de ser protestante (Luterano), numa cidade católica.
Esta era a época da Renascença e da Reforma Protestante. Por ter corpo frágil e pelas poucas condições financeiras da família, foi enviado ao seminário para seus estudos. Em setembro de 1588 Kepler passou o exame de admissão (bacharelado) da Universidade de Tübingen, mas só iniciou seus estudos lá em 17 de setembro de 1589, onde estudava teologia no seminário Stift.
Em 10 de agosto de 1591 foi aprovado no mestrado, completando os dois anos de estudos em Artes, que incluía grego, hebreu, astronomia e física. Iniciou então os estudos de teologia, estudando grego com Martin Crusius, matemática e astronomia com Michael Maestlin, aprendendo com este sobre Copérnico, embora seu mestre defendesse o modelo geocêntrico do Almagesto de Ptolomeu. Antes de completar seus estudos, Kepler foi convidado a ensinar matemática no seminário protestante (Stiftsschule) de Graz, na Áustria, onde chegou em 11 de abril de 1594. Seu trabalho, além de ensinar matemática, que se conectava com a astronomia, também incluía a posição de matemático e calendarista do distrito. Note que naquela época, o calendarista deveria prever o clima, dizendo a melhor data para plantar e colher, prever guerras e epidemias e mesmo eventos políticos. Kepler fazia os calendários porque era sua obrigação, mas tinhas sérias restrições à sua veracidade, dizendo por exemplo: “Os céus não podem causar muitos danos ao mais forte de dois inimigos, nem ajudar o mais fraco… Aquele bem preparado supera qualquer situação celeste desfavorável.” E mais, Kepler usava os calendários para instigar cuidados, disfarçados como prognósticos, para prevenir doenças.
Primeiro Livro No início de 1597, Kepler publica seu primeiro livro, Prodromus disserationum cosmographicarum continens mysterium cosmographicum de admirabili proportione orbium celestium deque causis coelorum numeri, magnitudinis, motuumque periodicorum genuinis et propiis, demonstratum per quinque regularia corpora geometrica, cujo título abreviado é Mysterium Cosmographicum (Mistérios do Universo). Neste livro defendia o heliocentrismo de Copérnico, e propunha que o tamanho de cada órbita planetária é estabelecido por um sólido geométrico (poliedro) circunscrito à órbita anterior.

Este modelo matemático poderia prever os tamanhos relativos das órbitas. Kepler enviou um exemplar para Tycho Brahe, que respondeu que existiam diferenças entre as previsões do modelo e suas medidas. Um exemplar enviado a Galileo, 8 anos mais velho que Kepler, fez este enviar uma pequena carta a Kepler agradecendo mas dizendo que ainda não havia lido, e dizendo que acreditava na teoria de Copérnico. Em setembro de 1598, o arquiduque da Áustria, príncipe Ferdinando de Habsburgo, líder da Contrarreforma Católica, fechou o colégio e a igreja protestante em Graz, e ordenou que todos os professores e padres deixassem a cidade imediatamente.
Kepler foi autorizado a retornar a cidade, como matemático do distrito, onde permaneceu até agosto de 1600, quando foi expulso definitivamente da cidade por recusar-se a se converter ao catolicismo. Em junho de 1599 o imperador Rudolph II, da Boêmia, contratou Tycho Brahe como matemático da corte em Praga.
Em janeiro de 1600 Kepler, então com 28 anos, visitou-o no castelo de Benatky, que o imperador tinha colocado à disposição de Tycho. Kepler sabia que somente com os dados de Tycho Brahe poderia resolver as diferenças entre os modelos e as observações. Tycho não acreditava no modelo de Copérnico por motivos teológicos, mas também porque acreditava que fosse possível medir a paralaxe das estrelas, que o modelo de Copérnico assumia à distância infinita.
A paralaxe das estrelas só foi medida em 1838, pela primeira vez, por Friedrich Wilhelm Bessel. Kepler já tinha observado eclipses e mesmo as estrelas, procurando medir a paralaxe, mas seus instrumentos eram muito rudes, e sua vista muita fraca. As descobertas Em 19 de outubro de 1600, Kepler, abandonado por seus antigos mestres por suas convicções na teoria heliocêntrica de Copérnico, e também por suas tendências Calvinistas, não aceitando os dogmas incondicionalmente, começou a trabalhar para Tycho Brahe em Praga.
Em setembro de 1601 Kepler retornou a Praga depois de uma visita a Graz para acertar a herança de seu sogro, e Tycho já havia instalado seus instrumentos, que haviam sido trazidos de Hveen. Tycho o apresentou ao imperador, que o contratou como assistente de Brahe. Logo depois, em 24 de outubro de 1601, Brahe morreu. Dois dias depois o imperador nomeou Kepler como matemático imperial, sucedendo Brahe na tarefa de calcular as Tabelas Rudolfinas, com a previsão das posições dos planetas. Kepler começou imediatamente a trabalhar no cálculo da órbita de Marte, e em 1602 descobriu a Lei das Áreas, mas não conseguiu fitar a forma da órbita. Se a órbita fosse circular, bastariam 3 observações, pois 3 pontos definem um círculo. Os pontos deveriam ser observados em oposição, já que em oposição é irrelevante se é a Terra ou o Sol que se movem, pois os três corpos estão alinhados. Tycho tinha observado 10 oposições de Marte entre 1580 e 1600, às quais Kepler depois adicionou as de 1602 e 1604. Naturalmente qualquer conjunto de 3 observações deveria resultar na mesma órbita. Como Marte é o planeta externo com maior excentricidade, dos conhecidos então, um círculo não fitava as observações. Mesmo introduzindo um equante Kepler não conseguia fitar as observações com erro menor que 8′, enquanto a precisão das observações de Tycho eram da ordem de 1′.

Em 1605 Kepler descobriu que a órbita era elíptica, com o Sol em um dos focos. Estes resultados foram publicados no Astronomia Nova, em 1609. Em 1604 Kepler completou o Astronomiae pars Optica (Ad Vitellionen Paralipomena, quibur Astronomiae Pars Optica traditur), considerado o livro fundamental da ótica, onde explicou a formação da imagem no olho humano, explicou como funciona uma câmara obscura, descobriu uma aproximação para a lei da refração, estudou o tamanho dos objetos celestes e os eclipses. Em 17 de outubro de 1604 Kepler observou a nova estrela (supernova) na constelação de Ophiucus, junto a Saturno, Júpiter e Marte, que estavam próximos, em conjunção. A estrela competia com Júpiter em brilho. Kepler imediatamente publicou um pequeno trabalho sobre ela, mas dois anos depois publicou um tratado, descrevendo o decaimento gradual de luminosidade, a cor, e considerações sobre a distância que a colocava junto com as outras estrelas.
Em 1610 Kepler leu o livro com as descobertas de Galileo usando o telescópio, e escreveu um longa carta em suporte publicada como Dissertatio cum Nuncio Sidereo (Conversa com o Mensageiro Sideral). Em agosto de 1610 ele usou um telescópio dado por Galileo ao duque da Bavária, Ernst de Cologne, para observar os satélites de Júpiter, publicando Narratio de Observatis Quatuor Jovis Satellitibus (Narração das Observações dos Quatro Satélites de Júpiter).

Estes tratados deram grande suporte a Galileo, cujas descobertas eram negadas por muitos. Os dois trabalhos foram republicados em Florença. Kepler também estudou as leis que governam a passagem da luz por lentes e sistemas de lentes, inclusive a magnificação e a redução da imagem, e como duas lentes convexas podem tornar objetos maiores e distintos, embora invertidos, que é o princípio do telescópio astronômico. Estudou também o telescópio de Galileo, com uma lente convergente como objetiva e uma lente divergente como ocular. Estes estudos foram publicados no Dioptrice, em 1611. Em 1612, com a morte do Imperador Rudolph II, que havia abdicado em 23 de maio de 1611, Kepler aceitou a posição de matemático e professor do colégio distrital em Linz. Lá publicou o primeiro trabalho sobre a cronologia e o ano do nascimento de Jesus, em alemão em 1613 e, ampliado, em Latim em 1614: De vero Anno, quo aeternus Dei Filius humanam naturam in Utero benedictae Virginis Mariae assumpsit (Sobre o Verdadeiro Ano em que o Filho de Deus assumiu a Natureza Humana no Útero da Sagrada Virgem Maria).
Neste trabalho Kepler demonstrou que o calendário Cristão estava em erro por cinco anos, pois Jesus tinha nascido em 4 aC, uma conclusão atualmente aceita. O argumento é que em 532 dC, o abade Dionysius Exigus assumiu que Cristo nascera no ano 754 da cidade de Roma, correspondente ao ano 46 do calendário Juliano, definindo-o como o ano um da era cristã. Entretanto vários historiadores afirmavam que o rei Herodes, que faleceu depois do nascimento de Cristo, morreu no ano 42 do calendário Juliano. Deste modo, o nascimento ocorrera em 41 do calendário Juliano. Novas publicações Entre 1617 e 1621 Kepler publicou os 7 volumes do Epitome Astronomiae Copernicanae (Compendium da Astronomia Copernicana), que se tornou a introdução mais importante à astronomia heliocêntrica, e um livro texto de grande uso. A primeira parte do Epitome, publicada em 1617, foi colocada no Index de livros proibidos pela Igreja Católica em 10 de maio de 1619. A proibição por parte da Igreja Católica às obras sobre o modelo heliocêntrico começou pelo fato de Galileo ter escrito seu livro Siderius Nuncius (Mensagem Celeste) em 1610, despertando o interesse do povo. A razão da proibição era que no Salmo 104:5 do Antigo Testamento da Bíblia, está escrito: “Deus colocou a Terra em suas fundações, para que nunca se mova”.
Em 1619 Kepler publicou Harmonices Mundi (Harmonia do Mundo), em que derivava que as distâncias heliocêntricas dos planetas e seus períodos estão relacionados pela Terceira Lei, que diz que o quadrado do período é proporcional ao cubo da distância média do planeta ao Sol. Esta lei foi descoberta por Kepler em 15 de maio de 1618. Perseguições Em 1615-16 houve uma caça às bruxas em sua região nativa, e ele defendeu sua mãe num processo em que ela era acusada de bruxarias. O processo se estendeu até 1920, quando ela foi liberada.
O ano de 1618 marcou o início da Guerra dos Trinta Anos, entre os Reformistas Protestantes e a Contra Reforma Católica, que devastou a região da Alemanha e Áustria. A posição de Kepler piorava, pois a Contra Reforma Católica aumentava a pressão sobre os protestantes na Alta Áustria, da qual Linz era a capital. Como Kepler era oficial da corte, ele está isento do decreto que bania todos os protestantes da província. Neste período Kepler estava imprimindo as Tabulae Rudolphinae baseadas nas observações de Tycho Brahe e calculadas de acordo com suas órbitas elípticas.
Estas tabelas incluiam a posição dos planetas e cálculos de eclipses. Quando uma rebelião ocorreu e Linz foi tomada, a oficina de impressão foi queimada, e com ela muito da edição já impressa. Kepler e sua família deixaram Linz em 1626. Sua família ficou em Regensburg, enquanto ele mudou-se para Ulm, para imprimir as Tabulae Rudolphinae, finalmente publicadas em 1627. Essas tabelas provaram-se precisas por um longo tempo, trazendo a aceitação geral ao sistema heliocêntrico. Apesar do nome de Kepler estar ligado à Astrologia, ele diz: “Meus corpos celestes não eram o nascimento de Mercúrio na sétima casa em quadratura com Marte, mas Copérnico e Tycho Brahe; sem sua observações, tudo o que eu pude trazer à luz estaria enterrado na escuridão’.’ Kepler então juntou-se à sua família em Regensburg, mas se mudou para Sagan em julho de 1928, como matemático do imperador e do duque de Friedland. Em uma viagem, foi acometido de uma doença aguda em Regensburg, Alemanha, onde faleceu em 15 de novembro de 1630.













