Os Pensadores (Le Penseur)
O Pensador (francês: Le Penseur) é uma das mais famosas esculturas de bronze do escultor francês Auguste Rodin. Retrata um homem em meditação soberba, lutando com uma poderosa força interna.
Originalmente chamado de O Poeta, a peça era parte de uma comissão do Museu de Arte Decorativa em Paris para criar um portal monumental baseada na Divina Comédia, de Dante Alighieri. Cada uma das estátuas na peça representavam um dos personagens principais do poema épico. O Pensador originalmente procurava retratar Dante em frente dos Portões do Inferno, ponderando seu grande poema. A escultura está nua porque Rodin queria uma figura heroica à la Michelangelo para representar o pensamento assim como a poesia.

François Auguste René Rodin |
|
|---|
Music & Lyrics |
Estudos Bíblicos |
Bíbia Sagrada |
O pensador original, na Porta do Inferno.
Rodin fez sua primeira versão por volta de 1880. A primeira estátua (O Pensador) em escala maior foi terminada em 1902, mas não foi apresentada ao público até 1904. Tornou-se propriedade da cidade de Paris graças a uma contribuição organizada pelos admiradores de Rodin e foi colocada em frente do Panteão em 1906. Em 1922, contudo, foi levada para o Hotel Biron, transformado no Musée Rodin. Mais de vinte cópias da escultura estão em museus em volta do mundo. Algumas destas cópias são versões ampliadas da obra original assim como as esculturas de diferentes proporções.
O Instituto Ricardo Brennand na cidade do Recife, Pernambuco, possui uma versão ampliada da obra original, exposta em seu acervo particular, na Galeria.
Johann Carl Friedrich Gauss 1777-1855
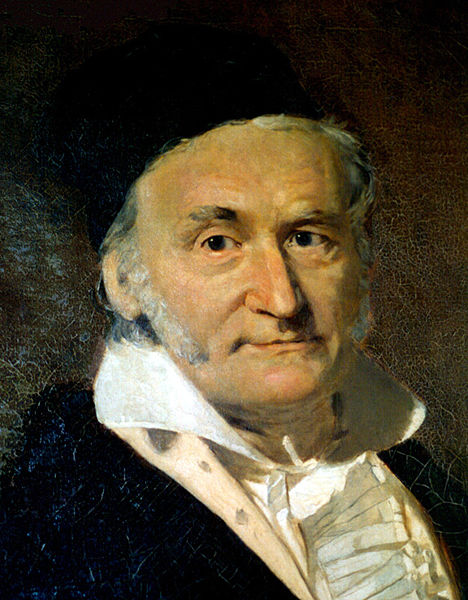
Carl Friedrich Gauss nasceu em 30 de abril de 1777 na cidade de Brunswick, hoje Alemanha. Trabalhou em diversos campos da matemática e da física dentre eles a teoria dos números, geometria diferencial, magnetismo, astronomia e ótica. Seu trabalho influenciou imensamente outras áreas. Aos sete anos de idade, Carl Friedrich começou a escola primária, e seu potencial foi notado quase imediatamente. Seu professor, Büttner, e seu assistente, Martin Bartels, ficaram pasmos quando Gauss somou os inteiros de 1 a 100 imediatamente, declarando que a soma era 50 pares de números, cada par somando 101.
Em 1788 Gauss começou o curso ginasial, com a ajuda de Büttner e Bartels com quem aprendeu alto alemão e latim. Depois de receber um estipêndio do Duque de Brunswick – Wolfenbüttel, em 1972, Gauss entrou em Brunswick Collegium Carolinum. Na academia, Gauss descobriu a lei do pressagio, o teorema de binômio e a aritmética – geometria fundamental, como também a lei de reciprocidade quadrática e o teorema de número primo. Em 1795 Gauss deixou Brunswick para estudar na Universidade de Göttingen.
Seu único amigo entre os estudante, durante anos, foi Farkas Bolyai. Gauss deixou Göttingen em 1798 sem um diploma, no entanto, antes realizou uma de suas mais importantes descobertas – a construção de umorreum polígono regular de 17 faces unicamente com régua e compasso. Este era o principal avanço neste campo desde o tempo de matemática grega e foi publicado como Seção VII do famoso trabalho de Gauss, Disquisitiones Arithmeticae, publicado em 1801. Gauss retornou a Brunswick em 1799 onde recebeu seu grau. O Duque de Brunswick tinha concordado em continuar o estipêndio de Gauss, e lhe pediu uma dissertação doutoral para a Universidade de Helmstedt. Gauss conhecia Pfaff que foi escolhido ser seu aconselhador e o ajudou na confecção da discussão do teorema fundamental de álgebra.
Em junho de 1801, Zach, um astrônomo, publicou as posições de orbital de Ceres, um novo planeta que foi descoberto por G Piazzi, um astrônomo italiano no dia 1 janeiro de 1801. Infelizmente, Piazzi só tinha podido observado 9 graus de sua órbita antes de desaparecesse atrás do Sol. Zach publicou diversas predições de suas posições, incluindo uma deferida por Gauss. Ceres foi redescoberto por Zach no dia 7 de dezembro de 1801, data quase exata onde Gauss predisse. Embora ele não descobriu seus métodos na ocasião, Gauss tinha usado o seu próprio método de aproximação de quadrados. Em junho de 1802 Gauss visitou Olbers o qual em março daquele ano, descobriu Pallas e Gauss investigou sua órbita. Olbers pediu para que Gauss fosse eleito o diretor do novo observatório proposto em Göttingen, mas nenhuma medida foi tomada. Gauss começou a se corresponder com Bessel porém não voltou a encontrá-lo até o ano de 1825.
Gauss casou-se com Johanna Ostoff no dia 9 de outubro de 1805. Apesar de ter uma vida pessoal feliz pela primeira vez, seu benfeitor, o Duque de Brunswick, foi morto lutando para o exército prussiano. Em 1807 Gauss deixou Brunswick para assumir a posição de diretor do observatório de Göttingen. Em 1808 seu pai vem a falecer e, um ano depois, sua esposa, que acabara de dar a luz a seu segundo filho, também morre. Gauss casou-se novamente no ano seguinte com Minna, a melhor amiga Johanna e, apesar de terem tidos três filhos, este matrimônio parecia ser uma conveniência de Gauss.

O trabalho de Gauss nunca parecia sofrer com sua tragédia pessoal. Publicou seu segundo livro, Theoria motus corporum coelestium em conicis de sectionibus ambientium de Solem, em 1809, o principal material sobre movimento de corpos celestiais, dividido em dois volumes. No primeiro volume ele discutiu equações diferencial, seções cônicas e órbitas elípticas, enquanto no segundo, a parte principal do trabalho, ele mostrou como calcular e então refinar a estimação da órbita de um planeta. As contribuições de Gauss para astronomia cessam a partir de 1817, apesar de ter feito observações até os 70 anos.
A maior parte do tempo de Gauss era gasto em um novo observatório, finalizado em 1816, porém ainda achara tempo para se dedicar a outros assuntos. As publicações realizadas por ele durante esse período incluem Disquisitiones generales circa seriem infinitam, um tratamento rigoroso de série e uma introdução da função hipergeometrica, Methodus nova integralium valores per approximationem inveniendi, Bestimmung der Genauigkeit der Beobachtungen, uma discussão sobre estatísticas estimadas, e Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodus nova tractata. Seu trabalho posterior foi inspirado por problemas geodésicos e estava principalmente preocupado com a teoria potencial.
Na realidade, em 1820, Gauss se achou cada vez mais interessado em geodésia, ciência que se ocupa da forma e da grandeza da terra ou de uma parte de sua superfície. Gauss, em 1818 recebeu a oportunidade do projeto geodésico do estado de Hanover e ficou grato em aceitá-lo e se encarregou da pesquisa. Fazia medidas durante o dia e as calculada durante à noite, usando sua extraordinária capacidade mental por cálculos . Escrevia regularmente a Schumacher, Olbers e Bessel, relatando seus progressos e discutindo os problemas. Por causa de suas pesquisas, Gauss inventou o heliotrópio que trabalhava refletindo os raios do Sol usando u e um pequeno telescópio pequeno. Porém, linhas básicas inexatas eram usadas para a pesquisa e uma rede não satisfatória de triângulos. Gauss desejou constantemente que lhe tivessem aconselhado a procurar alguma outra ocupação mas, apesar disso, ele publicou mais de 70 documentos entre 1820 e 1830.

Em 1822 Gauss ganhou o Prêmio da Universidade de Copenhague Theoria attractionis… junto com a ideia de traçar uma superfície sobre outra de forma que as duas sejam semehantesr nas partes menores. Este documento foi publicado em 1825 e conduziu a muitas publicações posteriores. O documento Theoria combinationis observationum erroribus minimis obnoxiae (1823), com seu suplemento (1828), foi dedicado a estatísticas matemáticas, em particular para o método dos quadrados.
No início de 1800 Gauss teve seu interesse voltado a possível existência de uma geometria não-Euclidiana. Discutiu este tópico com Farkas Bolyai e, por correspondência, com Gerling e Schumacher. Em uma revisão de um livro em 1816 ele discutiu provas das quais deduziram o axioma comparando-os com os axiomas Euclidianos, sugerindo que acreditassem na existência de uma geometria não-Euclidiana, embora isso ainda fosse bastante vago. Gauss confidenciou seus estudos a Schumacher, acreditando que, se admitisse em público a existência de tal geometria, sua reputação poderia ser abalada.
Em 1831 Farkas Bolyai enviou a Gauss o trabalho de seu filho János Bolyai sobre o assunto. Gauss respondeu: Exaltar isto poderia significar exaltar a mim mesmo Uma década depois, quando ele estava informado do trabalho de Lobachevsky sobre o assunto, elogiou seu caráter “genuinamente geométrico”, enquanto em uma carta para Schumacher em 1846, relatou que ele havia tido as mesmas convicções durante 54 anos, indicando que já sabia da existência de uma geometria não-Euclidiana desde os 15 anos de idade. Gauss teve seu principal interesse voltado para a geometria diferencial, e publicou muitos documentos sobre o assunto. Disquisitiones generales circa superficies curva (1828) era seu trabalho mais renomado neste campo. Na realidade, este documento subiu aos seus interesses geodésicos, mas conteve tais ideias geométricas como curvatura de Gauss. O papel também inclui o Teorema egregrium de Gauss: Se uma área em E³ pode ser desenvolvida (i.e. isometricamente traçado) em outra área de E³ os valores das curvaturas de Gauss são idênticos em pontos correspondentes.
O período de 1817-1832 foi particularmente infeliz para Gauss. Teve sua mãe doente em 1817, e ficou com ela até sua morte, em 1839. enquanto argumentava com sua esposa e a família dela se eles deveriam se mudar para Berlim pois tinha lhe oferecido uma vaga na Universidade de Berlim. Porém como Gauss não gostava de se mudar, acabou por ficar em Göttingen. Em 1831 morre a segunda esposa de Gauss, após uma longa doença. Em 1831, Wilhelm Weber chegou a Göttingen para preencher a cadeira de Tobias Mayer como professor de física. Gauss tinha trabalhado em física até 1831, publicando Uber ein neues allgemeines Grundgesetz der Mechanik e Principia generalia theoriae figurae fluidorum em aequilibrii de statu que discutia as forças de atração. Estes documentos estavam baseado na teoria de potencial de Gauss que provou de grande importância de seu trabalho na física e depois ele veio a acreditar no potencial de sua teoria e o método dos quadrados provinham ligações vitais entre a ciência e natureza. Em 1832, Gauss e Weber começaram a investigar a teoria de magnetismo terrestre depois de Alexander von Humboldt ter tentado obter ajuda de Gauss para fazer um grid de pontos de observação magnética ao redor da Terra.
Gauss estava entusiasmado por este projeto e, antes de 1840, já tinha escrito três importantes documentos sobre o assunto: Intensitas vis magneticae terrestris ad mensuram absolutam revocata (1832), Allgemeine Theorie des Erdmagnetismus (1839) e Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskräfte (1840). Estes documentos que tratavam das teorias atuais sobre o magnetismo terrestre, incluindo as idéias de Poisson, medida absoluta das força magnética e uma definição empírica de magnetismo terrestre.

A Allgemeine Theorie mostrou que só pode haver dois pólos no globo o que pode provar um importante teorema sobre a intensidade da componente horizontal da força magnética junto com o ângulo de inclinação. Gauss usou a equação de Laplace para ajudá-lo com cálculos, e acabou especificando um local para o pólo sul magnético. Humboldt inventara um calendário para observações de declinação magnética. Porém, assim que o novo observatório magnético que de Gauss ficou concluído (isso se consumou em 1833 – livre de todos os metais magnéticos). ele se pôs em alterar muitos dos procedimentos de Humboldt, o que não lhe agradou muito. Porém, as mudanças de Gauss obtiveram resultados mais precisos com menos esforço. Gauss e Weber alcançaram muitos no seis anos em que tiveram juntos.
Eles descobriram as leis de Kirchhoff, como também construíram um primitivo dispositivo de telégrafo que poderia enviar mensagens até uma distância de 5000 pés. Porém, este foi apenas um passatempo agradável para Gauss. Ele estava mais interessado na tarefa de estabelecer uma rede mundial de pontos de observação magnética. Esta ocupação produziu muitos resultados concretos. Foram fundados o Magnetischer Verein e seu jornal, e o atlas geomagnético foi publicado. Os resultados de Gauss e Weber eram publicados no próprio jornal periódico de Weber durante o período de 1836 a 1841.
Em 1837, Weber foi forçado a deixar Göttingen quando foi envolvido em uma disputa política e, neste período, diminuíram gradualmente as atividade de Gauss. Ele ainda escreveu cartas a respeito às descobertas de cientistas da mesma categoria que normalmente observam que ele tinha conhecido os métodos por anos mas nunca tinha sentido a necessidade de publicá-los. Às vezes ele parecia extremamente agradado com avanços feitos por outros matemáticos, particularmente o de Einstein e de Lobachevsky. Gauss passou os anos de 1845 a 1851 atualizando os fundos monetários da Universidade de Göttingen. Este trabalho lhe deu uma experiência em práticas financeiras, com isso, Gauss fez sua fortuna através de investimentos astutos em companhias privadas. Dois dos últimos estudantes doutorais de Gauss, Precentor de Moritz e Dedekind. Dedekind escreveram uma descrição sobre seu supervisor: … normalmente ele se sentava de modo confortável, olhando para baixo, ligeiramente se inclinou, com mãos dobradas sobre seu o colo dele. Ele falou bastante livremente, muito claramente, simplesmente e claramente: mas quando ele quis enfatizar um ponto de vista novo… então ele ergueu a cabeça dele, virada a um desses se sentando próximo a ele, e contemplou a ele com o bonito dele, penetrando olhos azuis durante a fala enfática. … Se ele procedesse de uma explicação de princípios ao desenvolvimento de fórmulas matemáticas, então ele se levantou, e em uma postura muito vertical imponente ele escreveu em um quadro-negro ao lado dele dentro o dele peculiarmente letra bonita: ele sempre teve sucesso por economia e arranjo deliberado dentro sobreviva com um espaço bastante pequeno. Em de quem conclusão cuidadosa ele colocou valor especial para exemplos numéricos, ele trouxe os dados requeridos em pouco desliza de papel. Gauss apresentou a conferência de jubileu dourada dele em 1849, cinquenta anos depois que o diploma dele tivesse sido concedido através de Universidade de Hemstedt. Era adequadamente uma variação na dissertação dele de 1799.
Da comunidade matemática só Jacobi e Dirichlet estavam presentes, mas Gauss recebeu muitas mensagens e honours. De 1850 onwards o trabalho de Gauss era novamente de quase tudo de uma natureza prática embora ele aprovou a tese doutoral de Riemann e ouviu a conferência probatória dele. A última troca científica conhecida dele estava com Gerling. Ele discutiu um pêndulo de Foucalt modificado em 1854. Ele também pôde assistir à abertura da ligação de estrada de ferro nova entre Hanover e Göttingen, mas isto provou ser a última excursão dele.
Friedrich Gauss morreu de manhã cedo, durante seu sono em 23 fevereiro, 1855 em Göttingen, Hanover, hoje Alemanha)

